
Читайте также:
|
Вычислить предел  .
.
Умножим и разделим на сопряженное выражение  , тогда
, тогда

Здесь старшая степень  - первая, поэтому
- первая, поэтому

Контрольные варианты к задаче 6
Вычислить пределы функции:
 . .
|  . .
|
 . .
|  . .
|
 . .
|  . .
|
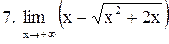 . .
| 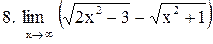 . .
|
 . .
|  . .
|
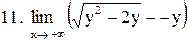 . .
| 
|
 . .
|  . .
|
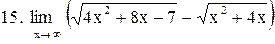 . .
|  . .
|
 . .
|  . .
|
 . .
|  . .
|

|  . .
|

|  . .
|
 . .
| 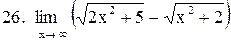 . .
|
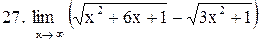 . .
|  . .
|
 . .
| 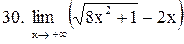 . .
|
З а д а ч а 7
Две бесконечно малые функции  при
при 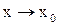 или
или  называются эквивалентными, если предел их отношения равен единице. Эквивалентность бесконечно малых функций записывается в виде
называются эквивалентными, если предел их отношения равен единице. Эквивалентность бесконечно малых функций записывается в виде  ~
~  .
.
Таким образом, если  , то
, то  ~
~  .
.
Таблица эквивалентных бесконечно малых функций
 ~ ~  , ,  . .
|
 ~ ~  , ,  . .
|
 ~ ~  , ,  . .
|
 ~ ~  , ,  . .
|
 ~ ~  , ,  . .
|
 ~ ~  , , 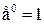 . .
|
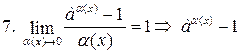 ~ ~  , ,  . .
|
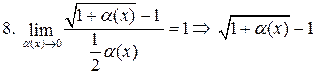 ~ ~ 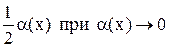 . .
|

|
Теорема. Предел отношения двух бесконечно малых не изменится, если одну или обе бесконечно малые заменить им эквивалентными, т. е. если 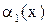 ~
~  и
и  ~
~  , то
, то 
Заметим, что с помощью эквивалентных бесконечно малых раскрывают неопределенность 
Пример 7
Вычислить предел 

Пример 8
Вычислить предел 

Дата добавления: 2015-10-21; просмотров: 63 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 3 | | | Пример 9 |