Пример 2

Типовой расчет

«Математический анализ»

З а д а ч а 1

Правило 1. Чтобы вычислить, нужно вместо переменной х поставить её предельное значение.

Если 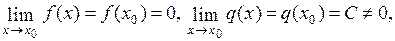то

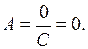
Если то.

Если то - неопределенность.

Правило 2. Чтобы раскрыть неопределенность 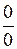в алгебраическом выражении, надо в числителе и знаменателе выделить множитель 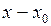, который стремится к нулю, и на него под знаком предела сократить.

Правило 3. Если в числителе и знаменателе стоят многочлены, то чтобы получить множитель 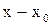, нужно многочлены разложить на множители.

Пример 1

При решении этой задачи необходимо знать формулы:

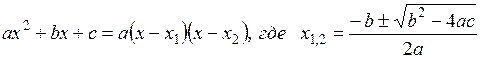
Вычислить предел 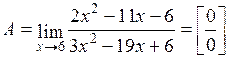.Действительно:

.

Найдем корни многочлена по формуле.

Тогда

.

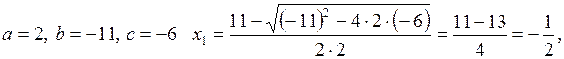
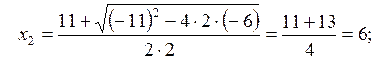
Анологично

Т.е.

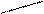
Контрольные варианты к задаче 1

Вычислить пределы функции:

.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.

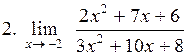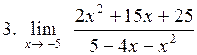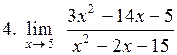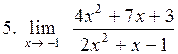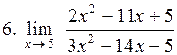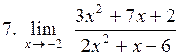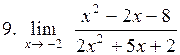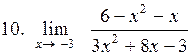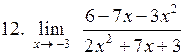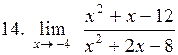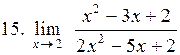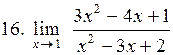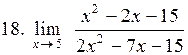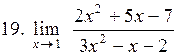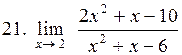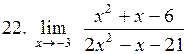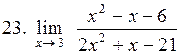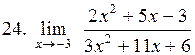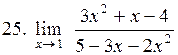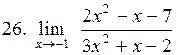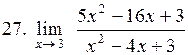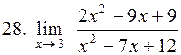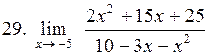З а д а ч а 2

При решении этой задачи необходимо знать формулы:

.

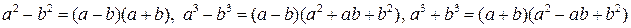
Пример 2

Вычислить

Найдем корни многочлена по формуле .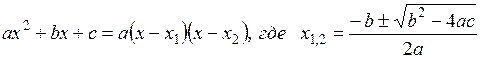

Тогда 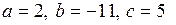и

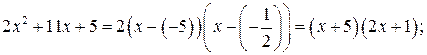
По формуле: 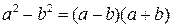имеем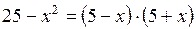

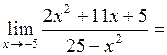
Контрольные варианты к задаче 2

Вычислить пределы функций:

1. .	2. .
3. 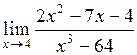.	4. .
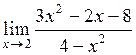
5.	6. .
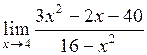
7.	8.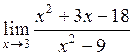
9.	10.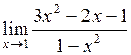
11.	12. .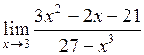
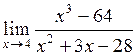
13.	14. .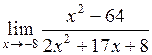
15. .	16. .
17. .	18. .
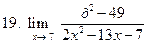.	20. .
21. 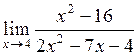.	22. .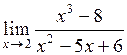
23. 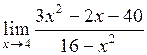.	24. .
25. 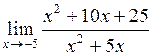.	26. .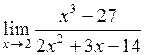
27. 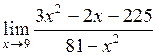.	28. .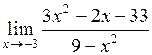
29. 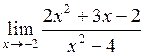.	30.

З а д а ч а 3

Если пр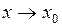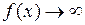и и 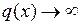, то отношение 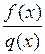представляет собой неопределенность 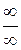. В этом случае рекомендуется числитель и знаменатель разделить почленно на старшую степень переменной х. При этом необходимо знать, что величина обратная бесконечно большой являетсябесконечно малой Величина обратная бесконечно малой является бесконечно большой

Дата добавления: 2015-10-21