Пример 3. Вычислить предел .

Вычислить предел .

.

Контрольные варианты к задаче 3

Вычислить пределы функций:

.	.
.	.
.	.
.	.
.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
	.
	.

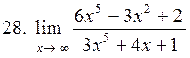З а д а ч а 4

Если пр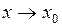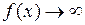и и 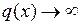, то отношение 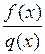представляет собой неопределенность . В этом случае рекомендуется числитель и знаменатель разделить почленно на старшую степень переменной х.

Пример 4

Вычислить предел .

.

Контрольные варианты к задаче 4

Вычислить пределы функций:

.	.
.	.
.	.
.	.
.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
	.
	.

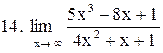З а д а ч а 5

При решении этой задачи необходимо знать формулы:

Пример 5

Вычислить предел .

Здесь старшая степень при n – вторая и - степень, поэтому

Контрольные варианты к задаче 5

Вычислить пределы числовых последовательностей:

.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
	.
.	.
.	.
.	.
.	.
.	.

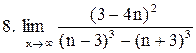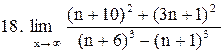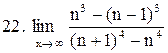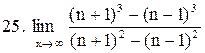З а д а ч а 6

Если при и , то разность представляет собой неопределенность . Чтобы раскрыть такую неопределенность, надо привести её к виду или .

Дата добавления: 2015-10-21