Capitolul III

3.1 Noţiune de stabilitate a sistemelor automate

Stabilitatea este un termen matematic care apreciază sistemul de funcţionare a sistemului automat.Pentru a studia stabilitatea sistemului se utilizează componenta liberă din soluţia ecuaţiei diferenţiale.

Componenta libera prezinta partea stînga a ecuaţiei diferenţiale, iar partea dreaptă este egală cu 0:

(a₀pⁿ+a₁p^n-1+...+a_n-1p+a_n)y=0

y≠0

Pentru studierea stabilitaţii se utilizează ecuaţia caracteristică care continue proprietăţile interne ale sistemului exprimate prin:

H(s)= ;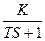

Dacă sistemul funcţioneaza atunci sistemul este stabil.Dacă sistemul nu funcţionează atunci sistemul nu este stabil.

Condiţiile necesare şi suficiente ale sistemului

Condiţiile de stabilitate sunt exprimate prin relaţia:

ye(t)=

Sistemul automat va fi stabil dacă toate rădăcinile ecuaţiei caracteristice vor avea partea reală negativă sau mai mică ca 0.

Sistemul va fi instabil dacă printre rădăcinile ecuaţiei caracteristice va fi una sau mai multe rădăcini cu partea reală pozitivă.

Sistemul e la limita de stabilitate dacă printre rădăcinile ecuaţiei caracteristice vor fi rădăcini nule şi imaginare.

Criteriile de stabilitate

Criterii de stabilitate sunt reguli (algoritmi) care permit de a determina stabilitatea sistemului după coeficienţii ecuaţiei caracteristice.

Criteriile permit de a determina localizarea rădăcinilor în planul rădăcinilor.

Condiţiile necesare de stabilitate:

- se utilizează ecuaţia caracteristică de gradul n cu coeficienţii cunoscuţi

- toţi coeficienţii ecuaţiei caracteristice a_0, a_1,...,a_n trebuie să fie pozitivi.

A(p)=a₀pⁿ+a₁ pⁿ+...+a_n-1p+a_n=0

- în ecuaţia caracteristică trebuie să fie prezente toate puterile lui a_n toate rădăcinile, fiind ecuaţie de gradul 1,2 aceste condiţii sunt şi suficiente la orce valuare ale coeficienţilor: 1) ;

2) ;

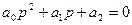Pentru ecuaţia de gradul 3 şi mai mare ca 3 condiţiile suficiente se determină utilizînd criterii de stabilitate. Sunt doua grupuri de criterii:

1.criterii algebrice - Routh şi Hurwitz

2.criterii frecvenţiale - Nyquist

Criteriul frecvenţial Nyquist este un criteriu practic sau experimental.Criteriul se aplică în bază pentru studierea stabilităţii sistemului automat deschis.Sistemul deschis este cu mult mai simplu ca cel închis. Prin definiţie se determină stabilitatea sistemului închis în baza evoluţiei studiate a sistemului deschis.

Дата добавления: 2015-10-21