Obiecte de reglare

Obiect de reglare este un proces industrial, tehnologic, un sistem de maşini etc. care necesită conducere (reglare).

Conducerea este o succesiune de comenzi sau un algoritm îndreptat spre obiect pentru al aduce în starea dorită.

p

OR

x y

OR – obiect de reglare,

x – mărime de intrare, mărime de comandă sau mărime de conducere.

y – mărime de ieşire, mărimea comandată, condusă, reglată.

p – mărimea de intrare şi e numită mărime perturbatorie,acţiunea acestei mărimi dereglează procesul.

Ansamblul compus din obiectul şi dispozitivul de reglare prezintă sistemul automat. Operatorul uman nu este inclus în acest sistem, dar are funcţia de a urmări procesul dat.Automatizarea duce la utilizarea raţională a surselor energetice şi materiale.

Principiile de reglare sau conducere

În automatică se utilizează următoarele principii de conducere:

1) Principiu de conducere cu sistemul deschis:

p

O

R

x U y

2) Principiu de conducere cu compensarea perturbaţiei

R

O

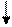
x E p y

E = x + p

Dacă asupra obiectului acţionează mai multe perturbaţii se alege acea care are o influenţă mai mare şi se compensează.

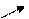
3) Principiu de conducere după eroare sau sistemul închis

- p

O

R

x E U y

-

Canalul de reacţie

Legătura inversă

E = x – y

E – eroarea sistemului şi atunci U = f (E) Reacţia rejectează (compensează) acţiunile perturbaţiei; stabilizează regimul de funcţionare a sistemului.

4) Principiu de conducere combinat

- p

O

R

x E U y E = x – y + p

-

Modele matematice ale elementelor şi sistemelor de reglare

Modelul matematic va fi prezentat prin: a) ecuaţia diferenţială

b) ecuaţia algebrică

c) funcţii de transfer

d) funcţii temporare

e) funcţii frecvenţiale

Ecuaţia diferenţială

MM

x (t) y (t)

Pentru a stabili relaţia dintre mărimile de intrare şi ieşire în domeniul timpului (diamico) se utilizează ecuaţia diferenţială.Prezentăm ecuaţia diferenţială în formă generală: F₁(y(t), (t), (t),..., y(t)ⁿ * t) = F₂(x(t), (t), (t),..., xⁿ(t) * t).

F₁, F₂, - funcţii neliniare

Ordinul ecuaţiei diferenţiale este egal cu numărul gradelor de libertate în spaţiu sau cu numărul de capacităţi în care se transformă energia, substanţa.

Elemente dinamice tipice

Un element dinamic tipic este modelul care este descris de o ecuaţie diferenţială nu mai mare de ordinul 2, şi se prezintă:

a₀ (t) + a₁ (t) + a₂ y(t) = b₀ (t) + b₁ (t) + b₂ x(t).

Din expresia dată obţinem 5 elemente tipice care ne exprimă proprietăţile interne a acestor elemente:

1. Element ideal

a₂ y(t) = b₂ x(t)

y(t) = kx(t) – descrie evoluţia în mediul ideal

Proprietatea elementului are parametrul k, care exprimă amplificarea sau atenuarea(nu are inerţie).

2. Element cu inerţie de ordinul 1

T (t) + y(t) = kx(t), ; T = ;[s]

3. Elemente cu acţiune integratoare

T_i (t) = x(t), T_i - constanta de timp de integrare

4. Elementul ideal şi real derivativ

y(t) = T_d (t), unde T_d – constanta de timp de derivare

T_p (t) + y(t) = T_d (t), unde T_p - constanta de timp de balast,parazitară,de filtrare

T_p ≈ (0,1... 0,125) T_d

5. Element oscilant amortizat

T² (t) + 2ξ T (t) + y(t) = kx(t) 0 < ξ < 1

1) cînd ξ = 0 – element oscilant neamortizat

2) cînd ξ ≥ 1 – element cu inerţie de ordinul 2

Elementul de inerţie de ordinul 2 se prezintă ca o conexiune a două elemente de inerţie de ordinul 1, la aceste 5 elemente se adaugă al 6-lea.

6. Element cu timp mort

Timp mort apare în două cazuri: a) timpul de transport

b) timpul de transformări fizico-chimice

Pe durata timpului mort nu este acţiunea sau mărimea de ieşire y(t) = kx (t - τ)

Funcţia de transfer

Funcţia de transfer este raportul mărimii de ieşire către cea de intrare,transformată după La Plase la condiţiile iniţiale nule.

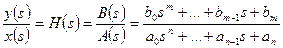
B(p) = 0; z_i, i =

Rădăcinile B(m) devin zerourile lui H(s) şi introduc în sistem, anticipat (acesta e efectul derivatelor la numărător).

Rădăcinile de A(p) le însemnăm prin P_j se numesc poii lui H(s), numitorul care prezintă proprietăţile de inerţie ale sistemului.

Дата добавления: 2015-10-21