Выполнение лабораторной работы. Этап I. Изучение моделей динамического хаоса

Этап I. Изучение моделей динамического хаоса

Запустить программу TIPSlab10 и изучить поведение предложенных моделей динамического хаоса, влияние начальных значений и параметров модели.

Этап II. Моделирование моделей динамического хаоса в пакете MatLab

Для численного моделирования систем дифференциальных уравнений представленных в нормальной форме Коши MatLAB предоставляет возможность две функции использующие метод Рунге-Кутта: ode23() - 2-3 порядка и ode45() -4-5 порядка. Вызов функций построен по следующему шаблону:

[<точки времени>,<значения переменных>]=ode23(<имя функции с моделью в НФК>, <начальное значение времени интегрирования>, <конечное значение времени>, <начальные значения переменных>, <точность интегрирования>);

Например, нам дано уравнение, не относящиеся к моделям хаоса, вида:

.

Преобразуем его к НФК: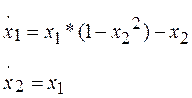

Переписываем эту систему уравнений в виде функции MatLAB:

function xx=dx(t, x)

xx(1)=x(1).*(1-x(2).^2)-x(2);

xx(2)=x(1);

Функция должна быть сохранена в файле с именем, совпадающим с именем функции и имеющим расширение ‘M’. Для того что бы MatLAB мог найти функцию необходимо указать путь до каталога, в который сохранен файл с его текстом. Сделать это можно с помощью команды path. При вызове команды path без параметров выдается список всех путей используемых в MatLAB. С помощью вызова path(matlabpath,’новый путь’) можно добавить новый путь в список путей.

Вызов ode23 или ode45 позволяет рассчитать значения процессов в модели:

[t, x] = ode23('dx',0,10,[-2, 2],1e-5).

Количество элементов в массиве x можно узнать с помощью команды size(x). Для построения графиков необходимо вызвать функции plot(t, x).

Для построения фазового портрета необходимо переписать значения отсчетов сигналов из двухмерного массива в вектора содержащие отсчеты только одного процесса.

Задания на моделирования моделей динамического хаоса

Дата добавления: 2015-10-21