Зависимость электрических свойств проводниковых материалов от внешних факторов

2.2.1. Температурная зависимость удельного сопротивления металлических проводников

Удельное сопротивление металлических проводников выражается эмпирическим правилом Маттиссена:

r _v = r_чист + r_прим; d r / dT = d r_чист / dT, (2.11)

где r_чист - это удельное сопротивление чистого металла, обусловленное рассеянием на тепловых колебаниях атомов решетки, оно зависит от температуры; r_прим - постоянная добавка, обусловленная рассеянием носителей заряда на примесях и дефектах кристаллической решетки; r_прим часто называют остаточным сопротивлением. Его оценивают по измерению при температуре жидкого азота (4,2 К). Обычно

r_прим = r_ост = (10^-2…10^-4) r_{300 К}. (2.12)

Измерение остаточного удельного сопротивления монокристаллических металлов дает возможность оценить степень их чистоты [8].

Типичная кривая изменения удельного сопротивления металлического проводника в зависимости от температуры представлена на рис. 2.1.

В области I, составляющей несколько кельвинов, у ряда металлов может наступить состояние сверхпроводимости, и на рисунке виден скачок удельного сопротивления при температуре Т _св. В реальных металлах при наличии дефектов и примесей наблюдается рост удельного сопротивления.

В пределах области II наблюдается быстрый рост удельного сопротивления r ~ Тⁿ, где остаточное n может быть до 5 и постепенно убывает с ростом температуры до 1 при Т = , где - температура Дебая. Она определяет максимальную частоту тепловых колебаний, которые могут возбуждаться в кристалле:

= h× n_max / K, (2.13)

где h - постоянная Планка; К - постоянная Больцмана; n_max - максимальная частота.

Область III − линейный T -участок температурной зависимости - у большинства металлов простирается до температур, близких к точке плавления. Исключение составляют ферромагнитные металлы. Вблизи точки плавления, т.е. в области IV, начало которой отмечено температурой , и в обычных металлах может наблюдаться некоторое отступление от линейной зависимости.

При переходе из твердого состояния в жидкое у большинства металлов наблюдается увеличение удельного сопротивления приблизительно в 1,5 - 2 раза - зона а на рис. 2.1, хотя у веществ со сложной кристаллической структурой (висмут, галлий) плавление сопровождается уменьшением r − зона б.

За счет введения примесей r_прим>>r_чист удельное сопротивление сплавов значительно выше, чем удельное сопротивление чистого металла. Повышение удельного сопротивления сплава по сравнению с чистым металлом отражает эмпирическое уравнение Нордхейма: r_спл = r_ме + A х ^.(1- х), где х − доля металла-примеси в сплаве; А − постоянная, характеризующая эффективность примесных атомов как рассеивающих центров.

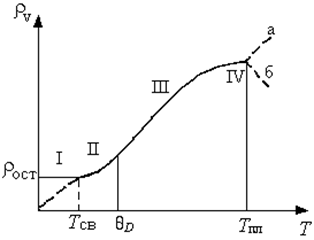
Рис. 2.1. Характер изменения удельного сопротивления проводника от температуры

Чем больше удельное сопротивление сплава, тем меньше его a_r. Это вытекает из того, что в твердых растворах r_прим значительно больше r_чист и не зависит от температуры. В соответствии с определением формула температурного коэффициента:

ТК . (2.14)

В концентрированных твердых растворах r применяют обычно на порядок больше r_чист. Поэтому может быть значительно ниже a_r чистого металла. На этом основано получение термостабильных проводящих материалов. Во многих случаях температурная зависимость удельного сопротивления сплавов более сложная, чем та, которая вытекает из правила Маттиссена. Температурный коэффициент сплавов может быть существенно ниже и даже отрицательным.

2.2.2. Зависимость удельного сопротивления проводниковых материалов от давления

Большое влияние на удельное сопротивление металлов и сплавов оказывают искажения, вызываемые напряженным состоянием. Однако степень этого влияния определяется характером напряжений. Например, при всестороннем сжатии у большинства металлов удельное сопротивление уменьшается. Это объясняется сближением атомов и уменьшением амплитуды тепловых колебаний решетки [5].

При упругом растяжении и кручении межатомные расстояния увеличиваются. Это сопровождается усилением рассеяния электронов и возрастанием r.

Влияние упругого растяжения или сжатия при условии пропускания тока вдоль действующей силы учитывается формулой

r = r₀×(1±js), (2.15)

где (¶ r/ ¶ s) - коэффициент удельного сопротивления по давлению; s - механическое напряжение в сечении образца. Знак плюс в формуле соответствует деформации при растяжении, а знак минус - при сжатии. Обычно коэффициент j = (1…5)×10^-11 Па^-1.

2.2.3. Сопротивление проводников на высоких частотах

На высоких частотах наблюдается неравномерное распределение электрического тока по сечению проводников: плотность тока максимальна на поверхности и убывает по мере проникновения в глубь проводника. Это явление получило названия поверхностного эффекта (СКИН-эффект). Приняв для проводящего полупространства направление тока за ось х, нормаль к поверхности за ось z и считая, что распределение остается неизменным вдоль оси х, получим следующее уравнение распределения тока по сечению проводника:

j_x ( z ) = j ₀exp(- z/ D),(2.16)

где j ₀ - плотность тока на поверхности; D - глубина проникновения поля в проводник, мм.

Глубина проникновения поля численно равна расстоянию, на котором амплитуда напряженности поля, а следовательно, и плотности тока уменьшается в е раз по отношению к своему значению на поверхности проводника. Значения глубины проникновения поля D связаны с физическими характеристиками материала выражением

, (2.17)

где f − частота поля, Гц; - магнитная постоянная; m- относительная магнитная проницаемость проводника; g− удельная проводимость проводника. В справочной литературе иногда приводятся упрощенные формулы для расчета D, например, для Аl:

.

В случае сильно выраженного поверхностного эффекта значение тока рассчитывается по формуле

, (2.18)

где П - периметр сечения проводника. Для провода круглого сечения П = p d.

На основании этого вводится понятие эквивалентной площади сечения проводника, занятой током при воздействии высокочастотного поля:

S _экв = PD = p d D. (2.19)

Поскольку центральная часть сечения проводника почти не используется, активное сопротивление проводника R при прохождении по нему переменного тока больше, чем его активное сопротивление R ₀ при постоянном токе. Коэффициент увеличения сопротивления k_R определяется по выражению

. (2.20)

Для проводников круглого сечения Δ. Для плоских проводников используют специальную характеристику − сопротивление квадрата поверхности , определяемое в омах из выражения , которое показывает, что активное сопротивление плоского проводника бесконечной толщины в случае поверхностного эффекта равно сопротивлению плоского проводника толщиной D для постоянного тока [5].

2.2.4 Свойства материалов в виде тонких плёнок

Свойства тонких плёнок отличаются от свойств массивных материалов, что связано со следующими факторами:

1) c методом получения тонких плёнок - наращивание из газовой фазы или молекулярного пучка послойно. Процесс наращивания идёт относительно медленно. Материалы металла при этом взаимодействуют с остаточными газами в вакууме. Происходит окисление. Окислы выделяются на границах зёрен и влияют на свойства материала;

2) с адгезионной способностью металлов. У разных металлов наблюдается разная адгезия к диэлектрическим подложкам. Такие металлы как Al, Cu, Ag, Аu - обладают плохой адгезией к диэлектрическим основаниям (адгезия - свойство сцепления). А такие металлы, как Титан, ванадий, Сr, Ni - обладают хорошей адгезией к диэлектрическим основаниям: керамика, стекло, ситалл. Плохая адгезия означает, что материалы высокой проводимости будут отслаиваться от диэлектрического основания, что вызывает нарушение надёжности работы интегральных схем. Поэтому напыление проводников и контактных площадок производится следующим порядком: на диэлектрическое основание напыляют тонкий подслой (~ 10нм) из материала с хорошей адгезией, а затем на подслой напыляют проводящий слой, затем защитное покрытие. Напыление обычно проводят на подогретую подложку, что улучшает адгезию;

3) из-за разности температурных коэффициентов линейного расширения диэлектрического основания и напыляемого слоя, неизбежно возникают внутренние напряжения, которые особенно заметны в толстых плёнках (~300¸500 мкм). Эти напряжения могут вызвать прогиб основания и плёнки становятся ненадёжными в эксплуатации;

4) в плёночных структурах металл-металл, металлическая подложка могут происходить разные физико-химические процессы, протекающие с большой скоростью при невысокой температуре Т=373°К. Эти процессы могут приводить к образованию новых соединений.

Пример: Если Al покрывать золотом,то образуется пурпурная чума AuAl₂ Это соединение вызывает разрушение с контактом.

Si +Au ® образуются легкоплавкие сплавы-эвтектики.

Si +Cu ®

При охлаждении эти сплавы кристаллизуются в виде игл и шипов и это нарушает планарность структуры. Если Al наносится на Si, то даже при низких температурах возможна диффузия Al в Si. Это вызывает изменение проводимости проводникового материала;

5) в тонких плёнках наблюдается отличие удельного сопротивления от удельного сопротивления массивного образца и правило Матиссена для тонких плёнок можно записать в таком виде:

r = r_т + r_прим +r_l

Появляется дополнительный механизм рассеяния, связанный с размерным эффектом r_l. Он появляется:

а) за счёт рассеяния электронов от границ плёнки, если толщина плёнки сравнима с длиной свободного пробега электронов;

б) за счёт строения плёнки и наблюдается в очень тонких плёнках. Если рассматривать рост тонких плёнок: плёнки имеют островковую структуру. Механизм прохождения тока по таким плёнкам - это туннельный эффект или термоэлектрическая эмиссия. Сопротивление складывается как сопротивление островков и промежутков между ними. Последнее сопротивление промежутков, определяется сопротивлением диэлектрических оснований. В результате результирующее сопротивление плёнки ® r_диэл.. Температурный коэффициент r < 0 как у диэлектриков. При увеличении толщины плёнки между островками появляются перемычки. Удельное сопротивление приближается к удельному сопротивлению п/п. При дальнейшем росте h удельное сопротивление приближается к удельному сопротивлению проводника.

в) В тонких плёнках наблюдается элетродиффузия, которая проявляется в том, что при протекании тока по тонкому проводнику происходит перемещение атомов кристаллической решётки причём атомы Al и Au перемещаются против поля, а платина по полю. Электродиффузия вызывает явления:

I) разрыв проводника, т.к. удаление металла начинается с самых тонких мест;

II) образование перемычек в местах скопления металла и короткого замыкания.

Электродиффузия уменьшает срок службы интегральных схем.

---

Дата добавления: 2015-10-21