Построение классификационных моделей

В данной работе при построении классификационных моделей использовались следующие методы анализа:

а) Деревья решений (С4.5 на рис.1)

б) CN2 классификация

в) Наивно-Байесовская классификация

г) Метод k-ближайших соседей

Задачей классификации является нахождение признаков объекта, которые позволяют объяснить его принадлежность тому или иному классу.

Поподробнее рассмотрим работу всех четырех методов:

а) Алгоритм построения дерева заключается в рекурсивном разбиении множества объектов на подмножества таким образом, чтобы в каждом подмножестве доминировали объекты одного класса, то есть используется древовидная структура из логических условий, которые в дальнейшем позволяют отнести объект к тому или иному классу.

Теперь рассмотрим как работает с данным классификатором схема, изображенная на рис.1. Поскольку система данных имеет слишком большое количество данных, то сделали случайную 30% выборку в Random Sampling в Data Sampler. После этого подключили сам классификатор С4.5 и вывели его на визуализаторы Classification Tree Viewer (рис.4.) и Classification Tree Graph (рис.5.)

Рис.4. Classification Tree Viewer

Рис.5. Classification Tree Graph

По описанию метода мы можем убедиться, что анализ представляет из себя древовидную структуру из условий. В блоке Classification Tree Viewer на вход поступила выборка из 1521 элемента (на рис.4 этого не видно). Столбец P(class) записывает вероятность правильности соотнесения объекта тому или иному классу. Например, по рис.4 при T13<=27.300 правильность классификации составляет 0.954 и объекты принадлежат классу Ozone со значением 0.

По Classification Tree Graph можно сказать следующее: красным цветом выделены объекты, отнесенные к классу 1., синим цветом – объекты класса 0., розовым и белым цветом выделены объекты, ошибка классификации которых высока. Например, возьмем для рассмотрения атрибут WSR20 (левый нижний угол, третий уровень снизу на рис.5), который выделен розовым цветом. При условии среднего значения данного атрибута<=3.900 получаем правильность классификации в 77.1% и он наиболее вероятно относится к классу 1.

б) Метод CN2 является методом построения классификации по ассоциативным правилам. По сути метод очень похож на предыдущий, где правила являются определенными условиями отбора данных. На схеме на рис.1 данному классификатору соответствует виджет CN2 и визуализатор CN2 Rules Viewer, работа которого представлена на рис.6. Первый столбец представляет собой длину ассоциативного правила (длину можно определить по количеству условий, заданных в колонке Rule); в колонке Rule Quality указывается правильность данной классификации; Coverage определяет количество объектов, покрываемых данным правилом.

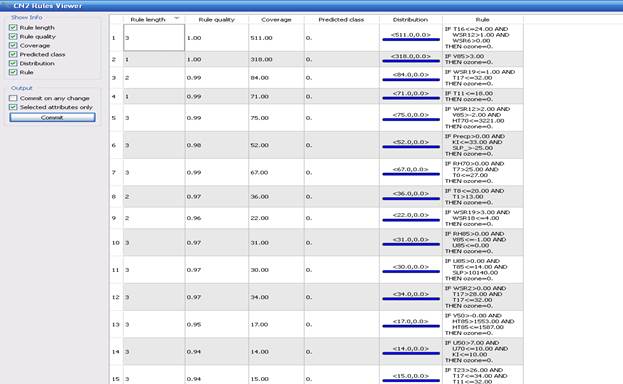
Рис.6. CN2 Rules Viewer

в) Наивно-Байесовская классификация работает основе расчёта условной вероятности принадлежности объекта к классу при условии равенства его атрибутов определённым значениям. При этом он исходит из предположений, что все атрибуты независимы и одинаково важны.

Визуализатором для Наивно-Байесовской классификации является виджет Nomogram, изображенный на рис.7.

Рис.7. Nomogram

В выплывающем списке Target Class слева стоит значение 0., следовательно, на данной номограмме мы по значениям атрибутов определяем, с какой условной вероятностью (по Байесу) атрибут при данном значении принадлежит классу Ozone со значением 0. Например, атрибут WSR0 со значением 6.6 с 72% вероятностью принадлежит классу Ozone со значением 0. Аналогично можно рассмотреть принадлежность к классу Ozone со значением 1., выбрав соответствующий пункт из Target Class.

г) Метод k-ближайших соседей работает по следующему принципу:

1) Производится отбор в исходной системе данных k-ближайших объектов (в нашем случае взяли 10).

2) Затем производится выбор класса объекта на основании 1). Класс формируется методом взвешивания голосований.

Данный метод не имеет визуализатора.

Классифицированные данные поступают на блок Test Learners, где происходит сравнение алгоритмов на обучающем множестве.

На рис.8, 9, 10, 11 представлена работа алгоритмов классификации при разных методах тестирования.

Рис.8. Результаты работы при тестировании Cross-Validation

Рис.9. Результаты работы при тестировании Leave-one-out

Рис.10. Результаты работы при тестировании Random Sampling

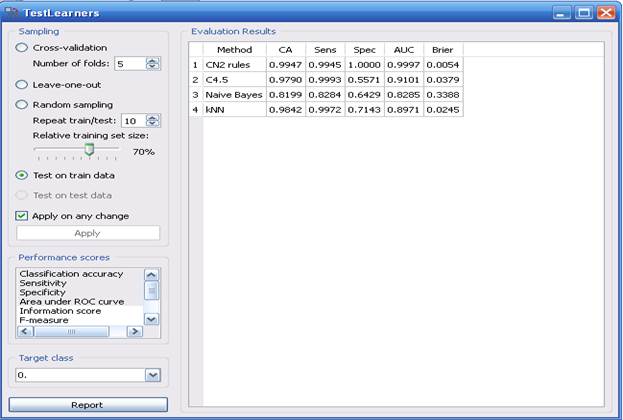
Рис.11. Результаты работы при тестировании Test on train data

Составим сводную таблицу, показывающую параметр CA (Classification Accurancy – правильность классификации).

Таблица 1.

Алгоритм	Способы оценивания качества алгоритма, %
Train test 70/30 10 folds one leave
C4.5	0.9790	0.9442	0.9224	0.9449
CN2	0.9947	0.9508	0.9447	0.9370
Naïve Bayes	0.8199	0.8144	0.7592	0.7953
k Nearest Neighbours	0.9842	0.9457	0.9289	0.9134

К блоку Test Learners подключается блок Confusion Matrix, который показывает сколько элементов или какой процент элементов классифицирован правильно для данного класса.

Дата добавления: 2015-10-21