В природе и обществе

В фейнмановских лекциях по физике приводится рассуждение, посвященное предсказуемости: "Обычно думают, что недетерминированность, невозможность предсказать будущее - это особенность квантовой механики, и именно с ней связывают представление о свободе воли и т.д. Но если бы даже наш мир был классическим, т.е. если бы законы механики были классическими, все равно из этого не следует, что те же или какие-то аналогичные представления не возникли бы. Да, конечно, с точки зрения классики, узнав местоположение и скорость всех частиц в мире (или в сосуде с газом), можно точно предсказать, что будет дальше. В этом смысле классический мир детерминирован. Но представьте теперь, что наша точность ограничена и что мы не знаем точно положение только одного из атомов; знаем, скажем, его с ошибкой в одну миллиардную. Тогда, если он столкнется с другим атомом, неопределенность в знании его координат после столкновения возрастет. А следующее столкновение еще сильнее увеличит ошибку. Так что если сначала ошибка и была еле заметной, то все равно вскоре она вырастает до огромнейшей неопределенности.

Ясно, что мы не можем по-настоящему предвидеть положение капель, если мы не знаем движения воды абсолютно точно.

Правильнее будет сказать, что для данной точности (сколь угодно большой, но конечной) можно всегда указать такой большой промежуток времени, что для него становится невозможным сделать предсказания. И этот промежуток (в этом вся соль) не так уж велик... Время с уменьшением ошибки растет только логарифмически, и оказывается, что за очень и очень малое время вся наша информация теряется".

Американское издание фейнмановских лекций вышло в 1963 г. В том же году в "Journal of the Atmospheric Sciences" появилась статья американского метеоролога Эдварда Лоренца, положившая начало новому направлению в естествознании - исследованию хаоса в детерминированных системах.

Новый механизм потери устойчивости был описан в 1963 г метеорологом Э. Лоренцом, который его наблюдал в численных экспериментах по моделированию возникновения турбулентности в процессе конвекции. Лоренц нашел область, обладающую необычными свойствами в трехмерном фазовом пространстве (в его случае координатами этого пространства являлись скорость и амплитуды двух температурных мод), которая существует при определенных условиях. Все траектории из окрестных областей притягиваются этой областью. Близкие траектории, попав в нее, расходятся и имеют очень сложную и запутанную структуру. Она была названа «странный аттрактор», так как, по определению, аттрактором, т.е. «притягателем» является притягивающее множество в фазовом пространстве, а в случае существования аттрактора, отличного от состояния равновесия и строго периодических колебаний, он называется странным.

Выбранное наугад решение в странном аттракторе Лоренца по прошествии достаточно большого времени пройдет достаточно близко к любой точке аттрактора, блуждая по нему. «Можно сказать, что странный аттрактор представляет собой бесконечную притягивающую линию, уложенную в конечном объеме фазового пространства. Переход системы на такой режим означает, что в ней наблюдаются сложные непериодические колебания, детали которых очень чувствительны к малому изменению начальных условий. Иными словами, две близкие в начальный момент времени траектории очень быстро разбегаются, что соответствует плохой предсказуемости течения по начальным условиям, которые всегда точно не известны». Долгосрочный динамический прогноз погоды из-за отсутствия точно заданных начальных условий представляет собой большую трудность. Еще до Лоренца в самом начале 60-х годов прошлого столетия советскими математиками Д.В. Аносовым и Я.Г. Синаем были установлены существование аттракторов с экспоненциально расходящимися фазовыми кривыми на них и устойчивость такого рода явлений.

Математический образ детерминированных непериодических процессов, для которых невозможен долгосрочный прогноз, назвали странными аттракторами. Эти аттракторы (от английского to attract - притягивать) действительно странные и очень красивые.

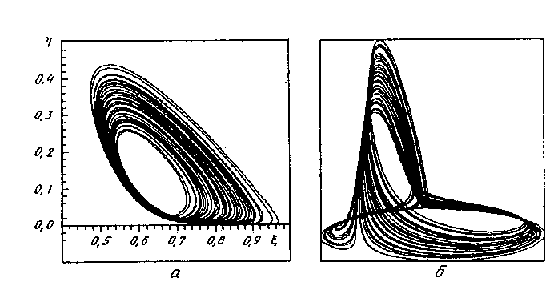
Рисунок 4.7. Странный аттрактор, соответствующий установившемуся режиму в модели, описывающей колебательную химическую реакцию. Точка, определяющая состояние объекта, принадлежит трехмерному пространству (математики говорят, что фазовое пространство этой динамической системы трехмерно). Представлены проекции аттрактора на две различные плоскости.

На рисунке 4.7. показан "портрет" такого аттрактора, описывающего колебания в некой химической реакции, которую моделировали на компьютере. Аттрактор на рис. 4.8. получен при обработке эксперимента по изучению знаменитой колебательной химической реакции Белоусова-Жаботинского.

Рисунок 4.8. Проекция аттрактора, полученная при экспериментальном исследовании реакции Белоусова-Жаботинского. Эта колебательная химическая реакция при определенных условиях может идти в хаотическом режиме.

Одним из результатов внедрения принципа универсального эволюционизма было возникновение синергетики. В классической науке господствовало убеждение, что материи свойственна тенденции к понижению степени ее упорядоченности, стремление к равновесию, что в энергетическом смысле означает хаотичность. Когда принцип эволюционизма, был распространен на другие уровни организации материи, противоречие стало еще заметнее. Стало очевидно, что для сохранения целостной не противоречивой картины мира нужно признать, что в природе действует не только разрушительный, но и созидательный принцип. Что материя способна самоорганизовываться и самоусложняться. На волне этих проблем возникла синергетика – теория самоорганизации. В настоящее время она развивается по нескольким направлениям: синергетика (Г. Хакен), неравновесная термодинамика (И. Пригожин) и др.

Общими положениями для всех для них являются следующие: процессы разрушения и созидания во Вселенной по меньшей мере равноправны; процессы созидания нарастания сложности и упорядоченности имеют единый алгоритм независимо от природы систем, в которых они осуществляются. Таким образом, синергетика ставит перед собой задачу выявление некого универсального механизма, с помощью которого осуществляется самоорганизация как в живой, так в неживой природе.

Вопросы и задания для закрепления знаний:

1. В чем заключаются особенности макроскопического метода описания действительности?

2. Прокомментируйте график потенциальной энергии взаимодействия двух молекул твердого тела.

3. В чем смысл распределения Максвелла для молекул газа по скоростям?

4. Как связаны теплота и механическая работа?

5. Опишите особенности неравновесных систем.

Дата добавления: 2015-10-21