И флуктуации. Закон возрастания энтропии

Представим, что в результате некоторого процесса в изолированной системе тело переходит из одного состояния в другое, а затем снова возвращается в исходное состояние. Процесс называется обратимым, если возможно осуществить обратный переход через те же промежуточные состояния так, чтобы не осталось никаких изменений в окружающих телах. Необратимыми называют процессы, в которых невозможен обратный переход без изменения в окружающих телах или в самом теле.

Любые процессы, сопровождаемые трением, являются необратимыми, поскольку при трении часть энергии превращается в тепловую. А значит, в окружающих телах происходят изменения. Любые реальные процессы невозможно представить без трения, следовательно, они являются необратимыми. Только идеальный механический процесс может происходить без трения и быть обратимым. Примером такого процесса может являться процесс колебания массивного маятника на длинном подвесе. Или другой пример из механики: падение упругого стального шара на упругую горизонтальную подставку. Такие процессы могут протекать сколь угодно долго и являются обратимыми.

Адиабатический процесс (так же, как и другие изопроцессы) является процессом квазистатическим. Все промежуточные состояния газа в этом процессе близки к состояниям термодинамического равновесия. Любая точка на адиабате описывает равновесное состояние.

Не всякий процесс, проведенный в адиабатической оболочке, то есть без теплообмена с окружающими телами, удовлетворяет этому условию. Примером неквазистатического процесса, в котором промежуточные состояния неравновесны, может служить расширение газа в пустоту. На рис. 10 изображена жесткая адиабатическая оболочка, состоящая из двух сообщающихся сосудов, разделенных вентилем K. В первоначальном состоянии газ заполняет один из сосудов, а в другом сосуде – вакуум. После открытия вентиля газ расширяется, заполняет оба сосуда, и устанавливается новое равновесное состояние. В этом процессе Q = 0, т.к. нет теплообмена с окружающими телами, и A = 0, т.к. оболочка не деформируема. Из первого закона термодинамики следует: ΔU = 0, то есть внутренняя энергия газа осталась неизменной. Так как внутренняя энергия идеального газа зависит только от температуры, температуры газа в начальном и конечном состояниях одинаковы – точки на плоскости (p, V), изображающие эти состояния, лежат на одной изотерме. Все промежуточные состояния газа неравновесны, и их нельзя изобразить на диаграмме.

Расширение газа в пустоту – пример необратимого процесса. Его нельзя провести в противоположном направлении.

 

Рисунок 4.5. Расширение газа в пустоту.

Феноменологическая термодинамика свела всю совокупность тепловых явлений в три начала без всякой модели вещества, т. е. они просто описывают все явления (отсюда и термин — феноменологическая). Клаузиус не только уточнил идеи Карно, но отказался от теплорода, объясняя природу теплоты в соответствии с концепцией атомизма. Важную роль в этом сыграла и новая абстрактная величина — энтропия (от греч. entropia — поворот, превращение), введенная им в 1865 г. Клаузиус определил понятие энтропии и показал, что в термически изолированных системах энтропия при обратимых процессах не изменяется, а при реальных и необратимых — растет всегда. Поэтому она является как бы мерой отклонения реальных процессов от идеальных. Энтропия, как характеристика состояния системы сыграла в развитии науки фундаментальную роль. Как каждому уровню высоты над поверхностью Земли отвечает своя потенциальная энергия, так и каждому состоянию термодинамической системы— своя энтропия. Как работа в поле силы тяжести не зависит от формы пути, а определяется только изменением потенциальной энергии, так и энтропия не зависит от вида процесса, определяясь только состоянием. Понятие энтропии как функции состояния было введено из рассмотрения квазистатических циклов. Число возможных способов осуществления какого-либо состояния называется статистическим весом W. Статистика показывает, что чем выше статистический вес данного состояния, тем оно более вероятно и ближе к равновесию. Убедиться в этом можно на простом примере, представленном на рис.4.6.

Рис.4.6. Модель возможных состояний системы

В состоянии с энергией U₁ = mgh сфероид может находиться только на вершине пирамиды. А в состоянии с энергией U₂ = 0 сфероид может располагаться в разных точках на плоскости. Т.е. первое состояние осуществляется лишь одним способом, а второе – практически неограниченным числом способов. Очевидно, что во втором случае сфероид может находиться в равновесии и это состояние наиболее вероятно. Следовательно: все равновесные состояния характеризуются максимальным статистическим весом. Существование системы в равновесном состоянии наиболее вероятно и самопроизвольно выйти из него она не может, потому что все естественные процессы необратимы. Это очевидно на примере расширения газа в пустоту, обратный процесс самопроизвольного сжатия газа мало вероятен. Установлено, что все естественные процессы протекают в сторону установления равновесия. Чтобы ответить на вопрос почему это происходит, рассмотрим вероятностную трактовку второго закона термодинамики. Количественной величиной равновесности состояния системы как раз и служит физическая величина – энтропия.

В 1878 году Л. Больцман дал вероятностную трактовку понятия энтропии. Он предложил рассматривать энтропию как меру статистического беспорядка в замкнутой термодинамической системе. Все самопроизвольно протекающие процессы в замкнутой системе, приближающие систему к состоянию равновесия и сопровождающиеся ростом энтропии, направлены в сторону увеличения вероятности состояния.

Всякое состояние макроскопической системы, содержащей большое число частиц, может быть реализовано многими способами. Термодинамическая вероятность W состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние. По определению термодинамическая вероятность W >> 1.

Согласно Больцману, энтропия S системы и термодинамическая вероятность W связаны между собой следующим образом:

S = k ln W,

где k = 1,38·10^–23 Дж/К – постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы.

Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия. Такие отклонения называются флуктуациями. В системах, содержащих большое число частиц, значительные отклонения от состояния равновесия имеют чрезвычайно малую вероятность.

Рост энтропии является общим свойством всех самопроизвольно протекающих необратимых процессов в изолированных термодинамических системах. При обратимых процессах в изолированных системах энтропия не изменяется:

ΔS ≥ 0.

Это соотношение принято называть законом возрастания энтропии.

При любых процессах, протекающих в термодинамических изолированных системах, энтропия либо остается неизменной, либо увеличивается.

Таким образом, энтропия указывает направление самопроизвольно протекающих процессов. Рост энтропии указывает на приближение системы к состоянию термодинамического равновесия. В состоянии равновесия энтропия принимает максимальное значение. Закон возрастания энтропии можно принять в качестве еще одной формулировки второго закона термодинамики.

Второе начало термодинамики претерпело эволюцию — от тепловой аксиомы, выражающей опытный факт о невозможности самопроизвольного перехода теплоты от холодного тела к горячему (1850), к принципу эквивалентности превращений (1854) и к принципу существования и возрастания энтропии (1865). Итак, в изолированной системе энтропия может только возрастать, что эквивалентно второму началу термодинамики.

Основоположники классической термодинамики — Кельвин и Клаузиус — считали, что ее начала годятся для любой изолированной системы, в том числе и для всей Вселенной. Отсюда — вывод о неизбежности ее «тепловой смерти», т.е. такого состояния, когда все процессы прекратятся, и мир перейдет в состояние термодинамического равновесия. Они не находили процессов, в которых энергия могла бы повышать свое качество, считали, что все тепловые явления самопроизвольно происходят только в одном направлении: горячие тела охлаждаются, холодные — сами по себе не нагреваются, т. е. распределение энергии необратимо. Но они отделяли это свойство мира от сохранения количества энергии при всех превращениях. Второе начало термодинамики указывает естественное направление изменения распределения энергии, не зависящее от количества энергии. Идеи Клаузиуса и Кельвина носили описательный характер, но вызвали дискуссии. Дальнейшее развитие принципа необратимости, принципа возрастания энтропии состояло в распространении этого принципа на Вселенную в целом, что и было сделано Клаузиусом. Итак, согласно второму началу все физические процессы протекают в направлении передачи тепла от более горячих тел к менее горячим, а это означает, что медленно, но верно идет процесс выравнивания температуры во Вселенной. Следовательно, в будущем ожидается исчезновение температурных различий и превращение всей мировой энергии в тепловую, равномерно распределенную во Вселенной. Вывод Клаузиуса был следующим:

1. Энергия мира постоянна.

2. Энтропия мира стремится к максимуму.

Таким образом, тепловая смерть Вселенной означает полное прекращение всех физических процессов вследствие перехода Вселенной в равновесное состояние с максимальной энтропией.

Сложные системы в отличие от простых, описываемых несколькими параметрами, состоят из большого числа переменных и большого числа связей между ними. В сложной системе появляется из-за внутренних взаимодействий много свойств, которых нет у ее частей (эмерджентные свойства), они — следствие целостности системы. На пути любой достаточно сложной системы к равновесию, которое характеризуется максимумом энтропии, встречаются обстоятельства, не позволяющие это сделать. В качестве таковых выступают граничные условия. Если они постоянны, например, поддерживают 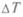на границах, то переменные состояния стремятся асимптотически к независимым от времени величинам, достигая квазистационарного или стационарного состояния.

Теорема о минимуме производства энтропии в стационарном неравновесном состоянии, сформулированная Пригожиным, отражает внутреннюю устойчивость неравновесных систем, ее своеобразную инерционность. Поэтому, если какие-то граничные условия не позволяют системе прийти в устойчивое равновесие, где она придет в состояние с минимальным производством энтропии. Этот вывод годится в случае независимости феноменологических коэффициентов (вязкости, диффузии, теплопроводности) от параметров среды, что справедливо при небольших значениях градиентов и линейных зависимостях между потоками и термодинамическими силами. Устойчивость стационарных состояний с минимальным производством энтропии связана с принципом, сформулированным в 1884 г. Ле Шателье и обобщенным в 1887 г. с точки зрения термодинамики немецким физиком Карлом Брауном.

Функция диссипации — это прирост энтропии за единицу времени в единице объема в открытых системах, а системы, в которых функция диссипации отлична от нуля, названы диссипативными. В таких системах энергия упорядоченного движения переходит в энергию неупорядоченного движения и, в конечном счете, в теплоту. Практически все системы являются такими, поскольку трение и прочие силы сопротивления приводят к диссипации энергии. Принцип локального равновесия и теорема о минимуме производства энтропии в равновесных состояниях были положены в основу термодинамики необратимых процессов.

Дата добавления: 2015-10-21