Теплота и механическая работа (закон сохранения энергии)

Температуру и количество теплоты как различные понятия первым определил Ламберт (1755). В том же году и М. В.Ломоносов указал, что температура тела — степень теплоты — определяется скоростью движения частиц, тогда как количество теплоты зависит от общего количества движения этих частиц, т.е. от их кинетической энергии.

Определение температуры через операцию измерения называется операционным. Для количественного определения нужно найти величину, обладающую свойством температуры — быть одинаковой у всех тел, находящихся в тепловом равновесии. Австрийский физик Л.Больцман установил (1866), что этим свойством обладает средняя кинетическая энергия поступательного движения молекул: где постоянная Больцмана Дж/К. Значит, температура — мера средней кинетической энергии поступательного движения молекул идеального газа.

Механический эквивалент теплоты вывел Р. Майер из данных об удельной теплоемкости газов при постоянных давлении 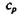и объеме 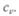Разность удельных теплоемкостей он приравнял работе, совершаемой при расширении газа, находящегося при постоянном давлении. И уравнение названо уравнением Майера [R — универсальная газовая постоянная, равная 2 кал/(моль • К)]. Воспользовавшись данными по удельной теплоемкости, Майер получил значение механического эквивалента теплоты I = 425 кГм/ккал (килограммометр на килокалорию), в системе СИ 1кал = 4,2 Дж.

Джоуль экспериментировал с проводниками электрического тока и измерял количество выделенной теплоты. Он открыл закон, по которому количество теплоты, выделенной током, пропорционально квадрату силы тока и сопротивлению. Этот же закон, независимо от Джоуля, получил в 1844 г. петербургский академик Э.Х.Ленц, поэтому он известен как закон Джоуля—Ленца. Джоуль провел много экспериментальных работ по исследованию тепловых явлений в гальванических цепях и выделению теплоты в химических реакциях.

Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом:

Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.

ΔU = Q – A.

Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме:

Q = ΔU + A.

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.

Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии.

Первый закон термодинамики применим к изопроцессам в газах. Такими процессами называют процессы, один из термодинамических параметров которых остается постоянным.

Изучение этих процессов привело к идее создания теплового двигателя. Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами.

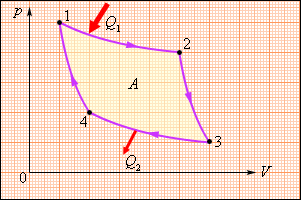
В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат. Этот круговой процесс сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 4.4).

 

Рисунок 4.4. Цикл Карно.

Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T₁. Газ изотермически расширяется, совершая работу A₁₂, при этом к газу подводится некоторое количество теплоты Q₁ = A₁₂. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A₂₃ > 0. Температура газа при адиабатическом расширении падает до значения T₂. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T₂ < T₁. Происходит процесс изотермического сжатия. Газ совершает работу A₃₄ < 0 и отдает тепло Q₂ < 0, равное произведенной работе A₃₄. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T₁, газ совершает работу A₄₁ < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:

A = A₁₂ + A₂₃ + A₃₄ + A₄₁.

На диаграмме (p, V) эта работа равна площади цикла.

С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя T₁ и холодильника T₂:

Цикл Карно замечателен тем, что на всех его участках отсутствует соприкосновение тел с различными температурами. Любое состояние рабочего тела (газа) на цикле является квазиравновесным, то есть бесконечно близким к состоянию теплового равновесия с окружающими телами (тепловыми резервуарами или термостатами). Цикл Карно исключает теплообмен при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника:

η_Карно = η_max.

Дата добавления: 2015-10-21