Обработка результатов эксперемента

В качестве оцениваемого критерия возьмем время достижения максимума током.

1. На основании показаний осциллографа и графика, построенного моделью, определим Y_мак и Y_мод:

№ опыта	№ сочетания факторов
	0,46	0,6	0,54	0,52	0,5	0,5
	0,48	0,44	0,5	0,58	0,48	0,54
	0,42	0,46	0,4	0,52	0,52	0,46
	0,44	0,48	0,46	0,48	0,62	0,4
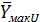
	0,45	0,495	0,475	0,525	0,530	0,475	0,492
	0,00067	0,00517	0,00357	0,00170	0,00387	0,00363	0,00310
	0,69	0,69	0,76	0,68	0,68	0,58	0,68

2. Определение влияния случайных факторов W на поведение макета:

Число степеней свободы: где — количество повторений каждого опыта.

Средние значения определяются по формуле:

Таким образом:

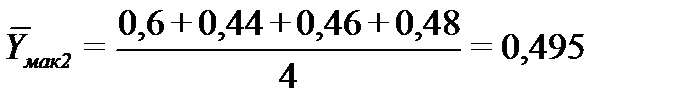
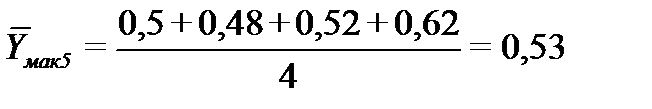
Среднее средних:

Дисперсии рассчитываются по формуле:

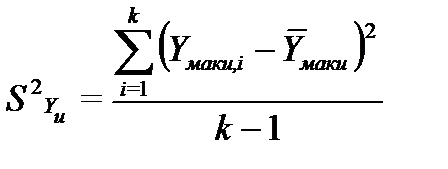
Таким образом:

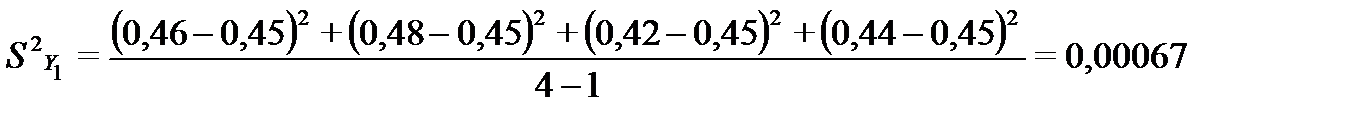
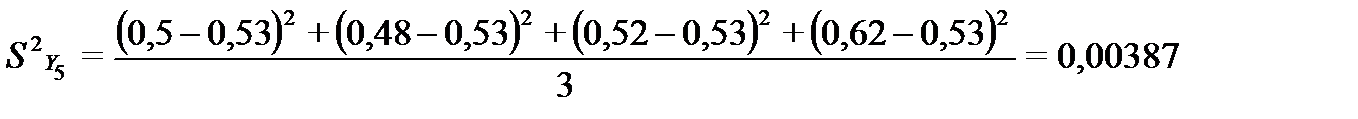
3. Проверка однородности результатов исследований при помощи - распределения:

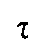Для объема выборки квантиль - распределения:

Проверка проводится по формуле:

а) 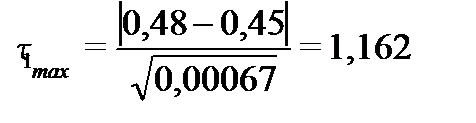и

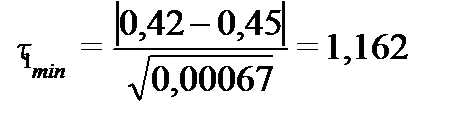
поскольку 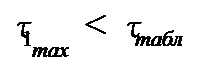и то в первом исследовании выбросов или ошибок не было.

б) и

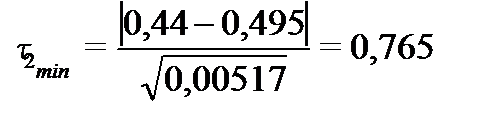
поскольку и то во втором исследовании выбросов или ошибок не было.

в) 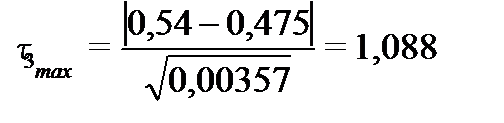и

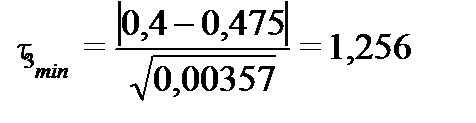
поскольку 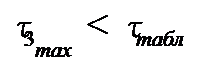и 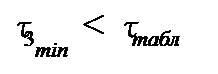то в третьем исследовании выбросов или ошибок не было.

г) 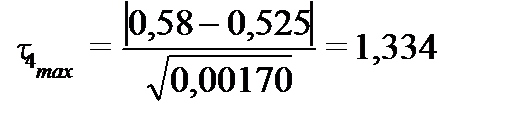и

поскольку и 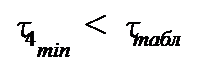то в четвертом исследовании выбросов или ошибок не было.

д) и

поскольку и 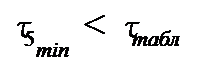то в пятом исследовании выбросов или ошибок не было.

е) и

поскольку и то в шестом исследовании выбросов или ошибок не было.

4. Оценка однородности дисперсий воспроизводимости по критерию Кохрена

производится по формуле:

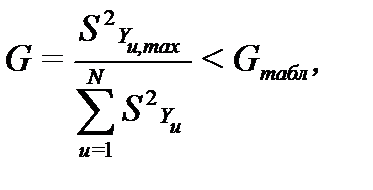
где - максимальная из дисперсий, а - табличное значение квантиля распределения Кохрена. Для и , табличное значение:

Поскольку то дисперсии однородны.

5. Оценка дисперсии воспроизводимости:

определена с числом степеней свободы

6. Определение коэффициентов:

- среднее модели:

Тогда коэффициенты:

Дисперсии коэффициентов регрессии вычисляются по формулам:

и

Численные значения:

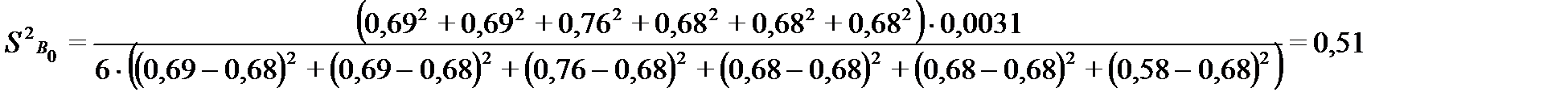
рассчитаны при числе степеней свободы

7. Значимости коэффициентов B₀ и B₁

Проверяется по критерию Стьюдента:

и

где - квантиль Стьюдента, определенный с числом степеней свободы 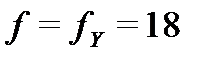и при

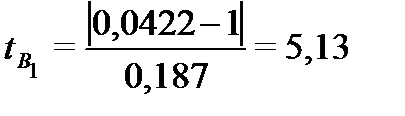
Поскольку то не существенно отличается от 0, но т. к. значит существенно отличается от 1. Из этого следует, что модель соответствует макету, но не идеально.

8. Адекватность модели и макета проверяется с помощью критерия Фишера путем сравнения дисперсии воспроизводимости с дисперсией адекватности которая вычисляется по формуле:

где

Численные значения

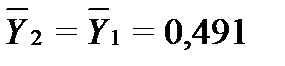
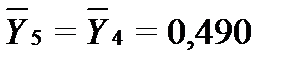
Дисперсия адекватности:

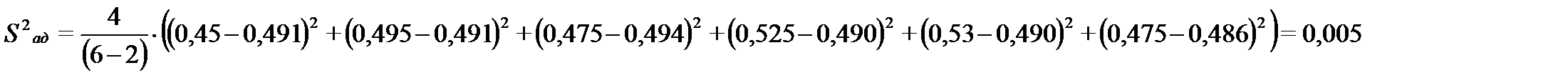
По критерию Фишера должно выполняться условие: 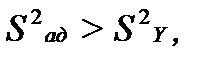поскольку то

где - квантиль распределения Фишера, определенный с и

Поскольку то модель адекватна макету.

ПОЛУЧЕНИЕ УРАВНЕНИЙ ДИНАМИЧЕСКИХ ИЛИ СТАТИЧЕСКИХ ПОКАЗАТЕЛЕЙ СИСТЕМЫ ЭЛЕКТРОПРИВОДА С ИСПОЛЬЗОВАНИЕМ МЕТОДОВ ТЕОРИИ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА.

В качестве функции цели Y возьмем время достижения током максимального значения. В качестве варируемых параметров , ,

Зависимость функции цели Y от факторов ищется в виде неполного квадратичного полинома:

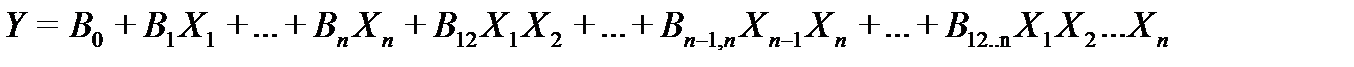
Для нахождения коэффициентов используется полный факторный эксперимент ПФЭ с варьированием факторов на двух уровнях. При этом проводится 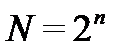опытов.

Для получим ПФЭ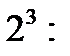

	+	—	—	—	+	+	+	—	0,523	0,527	0,00016
	+	+	—	—	—	—	+	+	0,575	0,5613	0,00016
	+	—	+	—	—	+	—	+	0,636	0,6388	0,00016
	+	+	+	—	+	—	—	—	0,666	0,6735	0,00016
	+	—	—	+	+	—	—	+	0,712	0,7118	0,00016
	+	+	—	+	—	+	—	—	0,736	0,7465	0,00016
	+	—	+	+	—	—	+	—	0,830	0,824	0,00016
	+	+	+	+	+	+	+	+	0,863	0,8588	0,00016
Н. Т.	+ 0	0,691	0,693	0,0012

Вид полинома:

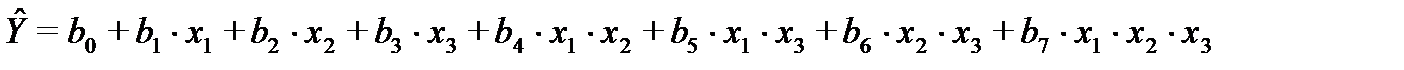
Коэффициенты рассчитываются по формуле:

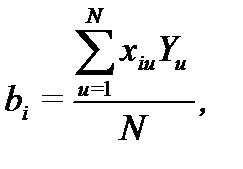
где 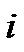- номер коэффициента; 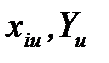- значение -ого фактора и функции цели в 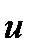-ом опыте плана.

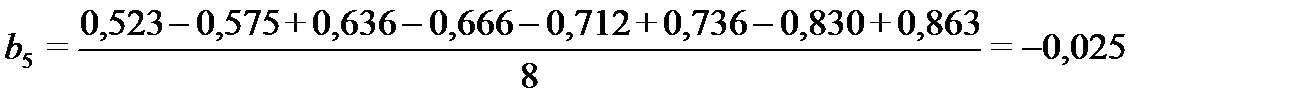
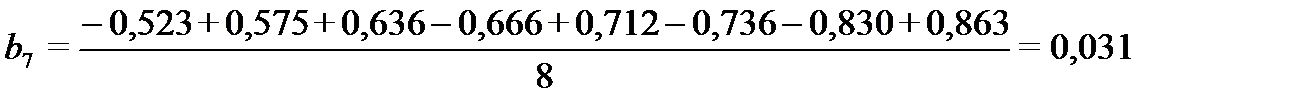
Дисперсии всех коэффициентов одинаковы и определяются через дисперсию воспроизводимости:

Значимость коэффициентов полинома определяется по условию:

где - табличное значение квантиля распределения Стьюдента. При числе степеней свободы и 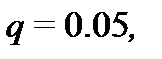квантиль распределения Стьюдента

Поскольку

Таким образом, окончательно полином имеет вид:

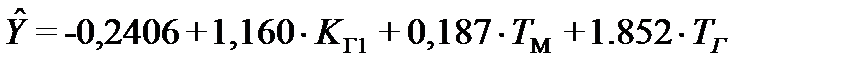
Проверка адекватности регрессии:

Соответствие оценивается по формуле:

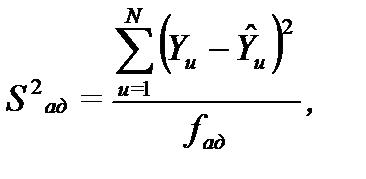
где число степеней свободы определяется как разность числа опытов N и числа l фактических членов полинома оставшихся после отбрасывания не значимых коэффициентов:

Для нашего случая:

и

Проверка адекватности выполняется по критерию Фишера

где 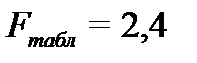- квантиль распределения Фишера, определенный с и

Поскольку регрессия адекватна.

Дисперсия предсказанного значения вычисляется для любой точки с координатами следующим образом:

где m — полное число членов полинома, не считая нулевого члена.

Для точки 1, получим:

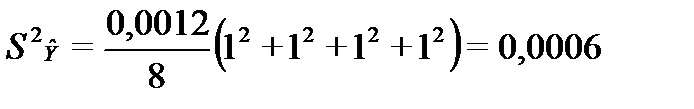
Для остальных точек аналогично.

Дата добавления: 2015-10-16