Теория теплоемкости Дебая

(*)

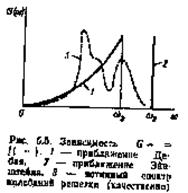
Формула (*), полученная Эйнштейном для теплоемкости, находится в хорошем согласии с экспериментом при Т=q_э, но при более низких температурах хорошего согласия уже не наблюдается. Рассчитанная по Эйнштейну теплоемкость падает с температурой быстрее, чем это имеет место в действительности (рис 1.). Эксперимент показал, что теплоемкость, по крайней мере, для диэлектриков, изменяется при низких температурах (при Т®0) не экспоненциально, а как Т³.

Расхождение эксперимента с теорией связано с тем, что в модели твердого тела Эйнштейна предполагалось, что каждый отдельно взятый атом совершает гармонические колебания независимо от других атомов с частотой w. На самом деле атомы в твердом теле не могут колебаться с одной и той же частотой, поскольку они сильно связаны между собой.

Следующий шаг в развитии квантовой теории теплоемкости был сделан Дебаем (1912 г.). Колебания сильно связанных между собой атомов мы ввели к совокупности слабо связанных волн распространяющихся во всем объеме кристалла с волновым вектором k и частотой ω(k,s). Каждой такой волне или нормальной моде колебаний мы сопоставили гармонический осциллятор, колеблющийся с частотой ω(к, s), в движении которого принимают участие все атомы твердого тела. Средняя энергия каждого такого осциллятора, в соответствии с формулой Планка, равна:

Поскольку каждый осциллятор в случае гармонического при­ближения колеблется независимо от других, то полная энергия колебаний кристалла (тепловая энергия) в общем случае при температуре Т, равна сумме энергий 3rN не взаимодействующих между собой гармонических осцилляторов (отдельных мод колебаний, формула (5.71):

Заменим суммирование по k интегрированием. Это можно сделать, поскольку число разрешенных значений волнового вектора k в зоне Бриллюэна [см. выражение (5,67)] очень велико и равно N, т. е. он меняется квазинепрерывно, а значит и частота ω(k) меняется квазинепрерывно от 0 до ω_max в акустической ветви (см. рис. 5.15). Тогда

где dN — число нормальных колебаний в интервале от k до k+dk и интегрирование производятся по зоне Бриллюэна. Для определения dk в k-пространстве выделим слой толщиной. dk, заключенный между сферами радиусов k и k+dk (рис. 6.4)

В модели Дебая предполагается, что скорость звука одинакова для всех длин волн и не зависит от направления поляризации, т. е. для трех акустических ветвей справедлив линейный закон дисперсии

(s=1,2,3)

где u^зв_s – скорость звука, константа. Тогда

и, следовательно, число нормальных колебаний в интервале между w и w+dw равно

отношение

представляет собой плотность мод колебаний решетки одной из поляризаций, т. е. число нормальных мод колебаний, соответствующих единичному интервалу частоты кристалла единичного объема. Функция r(w) в литературе также называется спектральной функцией распределения частот.

Поскольку в твердом теле возможны три типа акустических колебаний — одно полное со скоростью звука v_t и 2 поперечных со скоростью звука v_t (в изотропном случае скорости обеих поперечных мод одинаковы), то спектральная функция распределения в интервале dw в силу того, что плотность всех мод равна сумме плотностей отдельных мод, определяется выражением

где u_s, определяемая условием

есть скорость звука, усредненная по кристаллографическим направлениям и типам колебаний.

Используя (6.22), запишем формулу для Е_а в виде

В (6.24) Дебай заменил интегрирование по первой зоне Бриллюэна интегрированием по сфере радиуса k_d. выбираемой таким образом, чтобы эта сфера содержала ровно N разрешенных значений волновых векторов k. Это означает, что ее радиус определяется выражением

где - объем k-пространства, приходящийся на один разрешенный волновой вектор. Тогда

Если N/V=10²³ см-³, то k_D=2×10⁸ см^-1, что по порядку величины совпадает с размерами зоны Бриллюэна, а минимальная длина волны λ_D=2π/k_D=3×10^{-8 см имеет порядок постоянной} кристаллической решетки а. В решетке не могут распространяться волны с λ<2а,и максимальная или дебаевская частота колебаний, по которой берется интеграл в (6.16), в этой модели

с^-1

При сделанных Дебаем предположениях спектральная функция распределения для всех частот будет описываться выражением, которое в сумме дает

Формула для любых температур при известной функции распределения будет иметь вид:

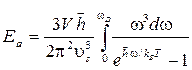
При вычислении интеграла удобно ввести новые переменные

;

Используя остальные выражения запишем формулу:

Это выражение носит название интерполяционной формулы Дебая, а

называют функцией Дебая. Эта формула интересна тем, что энергия, а следовательно, и теплоемкость C_v при всех температурах выражается через один параметр Q_D, называемый характеристической температурой твердого тела, или температурой Дебая. Ее физический смысл в том, что величина к_вQ_в=hw_D представляет максимальный квант энергии, способный возбудить колебания решетки. Оценка величины Q_D по формуле (6.30) с учетом результата (6.27) для w_D=7-10¹³ с-¹ показывает, что Q_D=100К. Температура Дебая, так же как и температура Эйнштейна, зависит от свойств вещества. Для большинства твердых тел она равна 100-400 К, хотя для таких веществ как бериллий (Q_D=1440 К) и алмаз (Q_D=2230 К) она аномально высока, что хорошо объясняется, как мы видели, повышенной «жесткостью» межатомных связей. Функцию Дебая явно вычислить нельзя, но аналитические выражения для энергии и теплоемкости можно получить в предельных случаяхнизких и высоких температур.

Высокие температуры hw<<k_BT или x<<1.

В этом случае в подынтегральном выражении мы можем разложить в ряд знаменатель, тогда после соответствующих преобразований теплоемкость будет равна:

т.е. она не зависит от температуры и соответствует закону Дюлонга и Пти.

Низкие температуры hw>>k_BT или x>>1

В этом случае в формуле (6:32) пределы интегрирования от 0 до Q_D/Т можно заменить пределами от 0 до ∞, поскольку такая замена не изменит существенным образом величины интеграла, который может быть вычислен:

Тогда энергия акустических колебаний будет равна

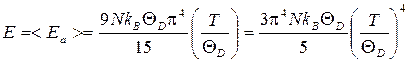
Формула (6.36) является точной при низких температурах, где правильно описывает зависимость энергии Е от температуры законом Т⁴. Теплоемкость при низких температурах, как следует из (6.36), описывается кубическим законом (Т³):

Эта зависимость хорошо согласуется с экспериментальными данными в узком интервале температур вблизи 0К. При более выоких температурах (Т<Qd) такого хорошего согласия не наблюдается. Это связано с тем, что при выводе формуы (6.32) для энергии были сделаны достаточно большие упрощения. В частности, задачи решались в гармоническом приближении, когда спектр колебаний можно разделить на независимые моды, что в реальных условиях, по крайней мере при высокой температуре, не может иметь места. Спектральная функция распределения G(w) была выбрана такой, что она существенно отличается от истинной функции распределения (кривые 1 и 3 на рис. 6.5), ни чем не обоснован резкий обрыв функии на частоте w_D. Использование истинного вида функции G(w), обычно вычисляемого на ЭВМ, приводит к хорошему совпадению вычисленных и экспериментальных данных в широкоминтервале температур.

До сих пор все наши рассуждения касались лишь акустических колебаний решетки, элементарные ячейки которой примитивны. В случае решеток с базисом необходимо в формуле для тепловой энергии, кроме вклада акустических колебаний учесть вклад оптических колебаний [см. формулы (6.13) и (6.15)]. Mы видели (см. рис. 5.15), что частота оптических колебаний слабо зависит от волнового вектора, поэтому к оптическим колебаниям лучше всего применима модель Эйнштейна.

30. ОСНОВЫ ЗОННОЙ ТЕОРИИ ТВЕРДЫХ ТЕЛ: ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ.

В основу классификации твер­дых тел могут быть положены различные признаки. По вели­чине удельной электропроводности все твердые тела можно разделить на три большие группы: металлы, диэлектрики и по­лупроводники. Металлы являются прекрасными проводниками электрического тока. Их удельная электропроводность при комнатной температуре колеблется от 10⁴ до 10^е Ом-¹-см^-1. Диэлектрики, наоборот, практически не проводят ток и исполь­зуются как изоляторы. Электропроводность (σ) этой группы ве­ществ меньше, чем 10^-10Ом^-1см^-1. Твердые тела, имеющие промежуточные значения σ, т. е. 10⁴- 10^—10 Ом-¹-см-¹, относят­ся к классу полупроводников. Из рис. 7.1 видно, что электропроводность различных веществ колеблется в очень широких пределах. Более того, одно и то же твердое тело в зависимо­сти от содержания примесей или дефектов в нем может иметь различную проводимость. Так, например, электропроводность кристаллического кремния из­меняется от 10³ до 10^-5 ' Ом^-1 см-¹, а а полупроводни­ка CdS заключена в интерва­ле 10³-10^-12 Ом-¹ см-¹. По­следний пример, в частности, показывает, что при переходе от одной группы веществ к другой значения электропро­водности могут перекрываться, поэтому классификация твер­дых тел по величине электро­проводности не является со­вершенно однозначной. Раз­личие между металлами, с одной стороны, и диэлектриками и полупроводниками — с другой проявляется достаточно четко в ходе температурных зависимостей электропроводности.

Для полупроводников и диэлектриков эта зависимость (в не­котором интервале температур) описывается выражением вида

т. е. возрастает с температурой по экспоненциальному закону. В то же время в металлах электропроводность уменьшается с ростом температуры:

В выражениях (7.1) и(7.2) σ_о, σ_о1, Т_о— некоторые константы. При термодинамических температурах, близких к абсолютному нулю, электропроводность многих металлов перестает изме­няться и имеет некоторое конечное значение. У некоторых ме­таллов возникает сверхпроводящее состояние. Диэлектрики и полупроводники характеризуются тем, что их электропровод­ность при Т→0 К обращается в нуль.

Рассмотренная нами в предыдущей главе модель свободных электронов, предложенная Друде и усовершенствованная Лорентцем, и, в особенности, модель Зоммерфельда, учитывающая квантовый характер электронного газа, достаточно хорошо объясняют ряд свойств металлов. Однако ни та, ни другая не дают ответа на вопрос: почему проводимость различных твер­дых тел изменяется в столь широких пределах? Почему одни вещества являются хорошими проводниками электрического тока, а другие — диэлектриками? Почему в некоторых твер­дых телах при низких термодинамических температурах возни­кает сверхпроводимость?

Отсутствие ответа на поставленные вопросы связано, оче­видно, с теми чрезмерными упрощениями, которые положены в основу модели свободных электронов. Основными из них явля­ются:

1) приближение свободных электронов, состоящее в том, что не учитывается влияние положительно заряженных ионов
на движение электронов в промежутках между столкнове­ниями;

2) приближение независимых электронов, предполагающее,
что отсутствует взаимодействие электронов между собой.

Основной источник трудностей, с которыми сталкиваются теории Друде — Лорентца и Зоммерфельда, связан с прибли­жением свободных электронов. Учет взаимодействия электро­нов с кристаллической решеткой и между собой делается в зонной теории твердых тел, основы которой будут рассмотрены ниже.

Дата добавления: 2015-10-16