Формальное описание и свойства бинарных отношений

Бинарным отношением R на множестве Ω называется подмножество R множества Ω ´ Ω (определение прямого произведение см. в разделе 3-2). Если пара á x, y ñвходит в R, т.е. á x, y ñÎ R, то пишут xRy, что читается так: «x находится в отношении R с y». Во многих случаях xRy интерпретируется как «x лучше y», «x доминирует y» и т.д.

Отношение называется пустым (обозначается знаком пустого множества Æ), если оно не выполняется ни для одной пары элементов Ω, т.е. соответствующее множество пар пусто. Отно-шение называется полным (обозначается U), если оно выполняется для всех пар элементов Ω. Отношение называется диагональным (обозначается Е), если оно выполняется для всех пар элементов Ω, состоящих из совпадающих элементов: xЕy ↔ x = y (знак ↔ здесь и далее означает «тогда и только тогда»). Отношение называется антидиагональным (обозначается ), если оно выполняется для всех пар элементов Ω, состоящих из несовпадающих элементов: x y ↔ x ¹ y.

Поскольку все отношения на Ω – подмножества одного и того же множества Ω ´ Ω, то мож-но обычным образом определить теоретико-множественные операции с отношениями: R ₁È R ₂ (объединение), R ₁Ç R ₂ (пересечение), (дополнение до полного отношения U). Вспоминая оп-ределение и свойства графиков (см. раздел 3-4), легко видеть, что бинарное отношение – как любое множество пар – является графиком. Поэтому все операции над графиками переносятся на бинарные отношения. Повторим здесь их вкратце.

Обратным к отношению R называется отношение R ^-1, определяемое условием: xR ^-1 y ↔ yRx. Произведением отношений R ₁ и R ₂ называется отношение, обозначаемое R ₁· R ₂, определяе-мое следующим образом: x (R ₁· R ₂) y, если существует z Î Ω, для которого xR ₁ z и zR ₂ y. Если R ₁ – отношение «быть братом», R ₂ – отношение «быть родителем», то произведение R ₁· R ₂ есть отно-шение «быть братом одного из родителей», т.е. «быть дядей». Ассоциативный закон, означаю-щий, что (A · B)· C = A ·(B · C), позволяет отказаться от расстановки скобок в произведениях и писать просто A · B · C и т.д; для совпадающих множителей можно писать Rⁿ.

Новой операцией является переход к двойственному отношению. Отношение R^d = на-зывается двойственным к отношению R.

Пример 1. Зададим следующее бинарное отношение R на множестве Ω = { a, b, c, d }: aRb, bRc, cRd, dRa, aRa, cRc, bRd, dRb. Построим отношение R^d, двойственное к R.

Шаг 1. Построим отношение , дополнительное к R. По определению дополнения в него вхо-дят все те и только те пары, которые не входят в R. Поэтому надо просто рассмотреть все пары элементов из Ω (включая пары с совпадающими элементами) и удалить из списка все те, кото-рые образуют отношение R (они приведены в списке). В нашем случае Ω = { a, b, c, d }, поэтому множество всех пар таково:

Ω ´ Ω ={á a, a ñ,á a, b ñ,á a, c ñ,á a, d ñ,á b, a ñ,á b, b ñ,á b, c ñ,á b, d ñ,á c, a ñ,á c, b ñ,á c, c ñ,á c, d ñ,á d, a ñ,á d, b ñ,á d, c ñ,á d, d ñ}

(всего 16 пар).

Исходное отношение R состоит из следующих пар:

R = {á a, b ñ,á b, c ñ,á c, d ñ,á d, a ñ,á a, a ñ,á c, c ñ,á b, d ñ,á d, b ñ}

(всего 8 пар). Дополнение к R состоит из всех пар, вошедших в полный список для Ω ´ Ω и не вошедших в список для R. Составим новый список для , просматривая по порядку все пары из полного списка, и добавляя в новый список те из них, которые не входят в R. Начинаем с па-ры á a, a ñ. Она входит в список для R (на 5-м месте) и поэтому не входит в . Следующая пара á a, b ñ также входит в список для R (на 1-м месте) и поэтому не входит в . Следующая пара á a, c ñ из полного списка не входят в R и поэтому включается в . Следующая пара ñ,á a, d ñ из полного списка также не входят в R и поэтому включается в . Продолжая этот процесс, получаем

= {á a, c ñ,á a, d ñ,á b, a ñ,á b, b ñ,á c, a ñ,á c, b ñ,á d, c ñ,á d, d ñ}.

Шаг 2. Построим отношение ()^-1, обратное к . По определению обратного отношения, надо взять все пары, входящие в исходное отношение, и поменять в них порядок на обратный (вмес-то пары á x, y ñ пара á y, x ñ; все пары вида á x, x ñ являются обратными к самим себе и поэтому входят в обратное отношение, если только входят в исходное отношение). В нашем случае исходным является отношение , построенное на шаге 1. Меняя порядок во всех парах из , получаем:

()^-1 ={á c, a ñ,á d, a ñ,á a, b ñ,á b, b ñ,á a, c ñ,á b, c ñ,á c, d ñ,á d, d ñ}.

Шаг 3. Отношение ()^-1, построенное на шаге 2, является требуемым отношением R^d ■

Задание 1. Построить отношения, двойственные к заданным.

01. Ω = { a, b, c, d, e, f }; aRa, aRd, aRe, aRf, bRa, cRc, bRc, fRc, bRe, eRa, eRc, eRf, fRa, dRf.

02. Ω = { a, b, c, d }; bRa, cRb, dRc, dRa, bRb, cRa, bRd, dRd.

03. Ω = { a, b, c, d, e, f }; aRa, aRd, aRe, aRf, bRa, cRc, bRc, fRc, bRe, eRa, eRc, eRf, fRa, dRf.

04. Ω = { a, b, c, d }; bRa, cRb, dRc, dRa, bRb, cRa, bRd, dRd.

05. Ω = { a, b, c, d, e, f }; aRb, bRd, cRf, dRe, eRb, aRc, bRf, fRc, cRd, cRc, eRd, fRa.

06. Ω = { a, b, c, d, e }; aRb, bRc, aRd, bRa, eRd, cRd, dRc.

07. Ω = { a, b, c, d, e, f }; aRb, bRd, cRf, dRe, eRb, aRc, bRf, fRc, cRd, cRc, eRd, fRa.

08. Ω = { a, b, c, d, e }; aRb, bRb, aRc, bRe, eRe, eRd, cRd, dRa.

09. Ω = { a, b, c, d, e, f }; aRb, bRd, cRf, dRe, eRb, aRc, bRf, fRc, cRd, cRc, eRd, fRa.

10. Ω = { a, b, c, d, e }; aRb, bRb, aRc, bRa, eRe, eRd, cRd, dRc.

12. Ω = { a, b, c, d, e }; aRb, bRb, aRc, bRa, eRe, eRd, cRd, dRc.

13. Ω = { a, b, c, d, e }; aRb, bRb, aRc, bRe, eRe, eRd, cRd, dRa.

14. Ω = { a, b, c, d, e, f }; aRb, bRd, cRf, dRe, eRb, aRc, bRf, fRc, cRd, cRc, eRd, fRa ■

Перейдём к описанию свойств бинарных отношений. Сначала опишем свойства, относя-щиеся к отдельным элементам Ω, затем – к их парам, тройкам и, наконец, к произвольным под-множествам Ω.

Отношение R называется рефлексивным, если для любого x Î Ω верно xRx,и антирефлек-сивным, если для любого x Î Ω неверно xRx (т.е. верно x x). Те же условия можно записать короче, пользуясь введёнными выше обозначениями: E Í R и R Í .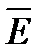

Отношение называется симметричным, если R Í R ^-1. Это значит, что из xRy следует, что yRx. Отношение называется асимметричным, если R Ç R ^-1 = Æ. Это значит, что из двух выра-жений xRy и yRx по меньшей мере одно неверно. Отношение «быть братом» не является ни сим-метричным, ни асимметричным. Действительно, если Пётр – брат Фёдора, то Фёдор – брат Пет-ра; но если Игорь – брат Ольги, то неверно, что Ольга – брат Игоря. Отношение называется ан-тисимметричным, если R Ç R ^-1 Í Е. Это значит, что xRy и yRx вместе выполняются только тог-да, когда x = y, или эквивалентно: из xRy и yRz следует, что x = y.

Отношение называется транзитивным, если R ²Í R, или эквивалентно: из xRy и yRz сле-дует, что xRz. Отноше­ние R называется отрицательно транзитивным, если его допол­нение транзитивно. Отношение R называется сильно транзитивным, если оно одно­временно транзитивно и отрицательно транзитивно.

Отношение называется ацикличным, если для любого k = 1, 2,... R^k Ç R ^-1 = Æ, или эквивалентно: из x ₁ Rx ₂, x ₂ Rx ₃, …, x_{k – 1} Rx_k следует, что x_k x ₁.

Ацикличность и транзитивность отношений особенно важны при выборе альтернатив, так как эти свойства выражают некоторые естественные взаимосвязи между объектами. Действи-тельно, если х в каком-либо смысле лучше, чем у, а у вэтом же смысле лучше, чем z, то естест-венно считать, что в этом смысле х лучше, чем z (транзитивность), и во всяком случае z не луч-ше x (ацикличность).

Некоторые свойсва отношений оказываются связанными. Приведём простое

Утверждение 1. Если отношение R не антифрексивно, то оно не асимметрично и не ацик-лично.

Действительно, если хотя бы для одного элемента x выполнено xRx, то по определению обратного отношения выполнено xR ^-1 x, откуда следует, чтопара á x, x ñÎ R∩R ^-1, т.е. R∩R ^-1 ≠ Æ. По определению это значит, что отношение R не асимметрично. Далее, пара xRx представляет со-бой цикл длины 1 и, значит, отношение R не ациклично ■

Пример 2. Пусть бинарное отношение R на множестве Ω = { a, b, c, d, e } таково: aRb, bRb, aRc, bRe, eRe, eRd, cRd, dRa. Обладает ли это отношение свойствами:

рефлексивности;

aсимметричности;

ацикличности?

1. Поскольку не выполнено aRa, то данное отношение рефлексивным не является.

2. Поскольку имеет место bRb, то отношение не антирефлексивно. В силу утверждения 1 отно-шение R не асимметрично и не ациклично ■

Пример 3. Пусть бинарное отношение R на множестве Ω = { a, b, c, d, e } таково: aRb, bRb, aRc, bRa, eRe, eRd, cRd, dRc. Обладает ли это отношение свойствами:

антирефлексивности;

асимметричности;

транзитивности?

1. Поскольку имеет место bRb, то отношение R не является антирефлексивным.

2. Поскольку отношение R не является антирефлексивным, то в силу утверждения 1 отно-шение R не асимметрично.

3. Поскольку верно aRc и cRd,то из транзитивности R должно следовать aRd. Поскольку aRd в заданном списке отсутствует, то отсюда следует, что данное отношение не транзитивно ■

Дата добавления: 2015-10-16