Ведущий вал

Рассмотрим общий случай нагружения вала вращающим моментом Т₁, результирующим усилием в ременной передаче Q и тремя составляющими усилия в зацеплении (1). Причем осевая составляющая создает сосредоточенный момент на плече, равном радиусу делительной окружности m= F_a d₁/2. Напомним, что для прямозубой и шевронной передач осевая составляющая F_a в приведенных ниже формулах будет равна 0 (рис.12,а).

Эпюра крутящих моментов показана на рис.12,б. Крутящий момент создается скручивающим моментом Т₁, который подается на вал через ременную передачу и снимается в зубчатом зацеплении.

Для построения эпюр изгибающих моментов сначала определим реактивные силы в подшипниковых опорах. Пользуясь принципом суперпозиций, определяем горизонтальные X_I,X_II и вертикальные Y_I,Y_II составляющие реакций. Расчетная схема нагружения вала в вертикальной плоскости приведена на рис.12, в. Составляем уравнения равновесия моментов сил, действующих на вал, относительно опорных точек I,II и преобразуем их относительно неизвестных

Y_I = (Q(l_p+l_b) - F_rl_p/2 – m)/l_p; (15)

Y_II = (Ql_b + F_rl_p/2 – m)/l_p. (16)

Производя аналогичные выкладки для расчетной схемы вала в горизонтальной плоскости, представленной на рис.12,д, определяем опроные реакции в горизонтальной плоскости

X_I = X_II = F_t/2. (17)

Значения моментов на границах расчетных участков и эпюра изгибающих моментов М_из^в приведены на рис.12,г.

В горизонтальной плоскости на вал действует только окружное усилие. Значения моментов на границах расчетных участков и эпюра изгибающих моментов М_из^г приведены на рис.12,е.

Суммарный изгибающий момент М_из в любом сечении определяют по правилу геометрического сложения

(18)

4.1.2. Тихоходный вал

Рассмотрим расчетные схемы вала на изгиб в вертикальной (рис.13,в) и горизонтальной (рис.13,д) плоскостях. В вертикальной плоскости на вал действует радиальная и осевая составляющие усилия в зацеплении. Осевая составляющая как и ранее создает сосредоточенный момент m= F_a d₂/2. Вращающий момент Т₂ подается на вал через зубчатую передачу и снисается на выходном конце, в муфте.

Опорные реакции Y_I,Y_II в вертикальные плоскости (рис.13,в) определяем решением уравнений равновесия моментов относительно опор

Y_I = (m - F_rl_p/2)/ l_p; (19)

Y_II = (F_rl_p/2 + m)/ l_p. (20)

Производя аналогичные выкладки для расчетной схемы вала в горизонтальной плоскости, представленной на рис.13,д, определяем опроные реакции в горизонтальной плоскости

X_I = X_II = F_t/2. (21)

Значения моментов в вертикальной и горизонтальной плоскостях на границах расчетных участков и эпюры соответствующих изгибающих моментов М_из^в, М_из^г приведены на рис.13.в, 13,е. Суммарный изгибающий момент определяется по формуле (18).

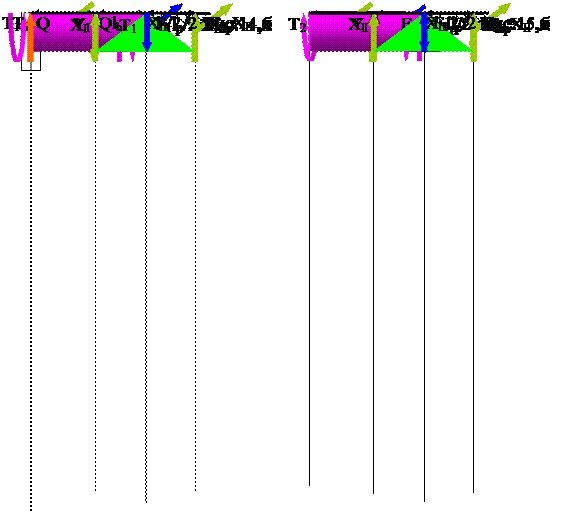
Расчет внутренних усилий на быстроходном и тихоходном валах прямозубой и шевронной передач выполняется в той же последовательности. На рис.14 и 15 приведены расчетные схемы и эпюры крутящих и изгибающих моментов для соответственно быстроходного и тихоходного валов.

Дата добавления: 2015-10-16