Теорема о циркуляции

1. Понятие циркуляции.

Циркуляцией вектора B по заданному замкнутому контуру L называется следующий интеграл по этому контуру:

Теорема о циркуляции вектора B (закон полного магнитного поля в вакууме):циркуляция вектора B по произвольному замкнутому контуру равна произведению магнитной постоянной µ₀ на алгебраическую сумму токов, охватываемых этим контуром.

Циркуляция напряженности эл поля всегда равна 0,следовательно,электростатическое поле потенциально и может быть ох-на потенциалом. Циркуляция магнитной индукции отлична от нуля, если контур, по которому берется циркуляция, охватывает ток.

3. Закон полного тока.

Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов (токов намагниченности), охватываемых этим контуром, умноженной на магнитную постоянную:

Циркуляция вектора H по произвольному замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых этим контуром. Циркуляция вектора намагниченности J по произвольному замкнутому контуру равна току намагниченности I_м, охватываемому этим контуром

2. Примеры применения теоремы

Магнитное поле бесконечного проводника с током:

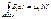Магнитное поле соленоида:

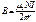
Магнитное поле тороида в вакууме:

17. Заряд, движущийся в магнитном поле.

1. Магнитное поле движущегося заряда.

Напряженность магнитного поля движущегося заряда также можно определить, используя закон Био – Савара – Лапласа. Таким образом Idl = jSdl = nqvSdl = nqdVv = Nqv, где dV – объем элемента проводника dl, N – полное число частиц в отрезке dl проводника.

2. Действие магнитного поля на движущийся заряд.

Силу действия магнитного поля на движущийся заряд можно найти исходя из закона Ампера. Пусть по проводнику длиной dl за промежуток времени dt проходит n элементарных зарядов величиной q, т.е. через проводник протекает ток, сила которого I=nq/dt.

Сила Лоренца, действующая со стороны магнитного поля на движущийся заряд, равна (в скалярной и векторной формах).

Так как сила Лоренца всегда направлена перпендикулярно вектору скорости частицы, то она не изменяет величину скорости, а изменяет лишь направление движения частицы, т.е. по физической сути является центростремительной силой. Действие этой силы не приводит к изменению энергии заряженной частицы, т.е. эта сила не совершает работы.

3. Варианты движения заряженных частиц в магнитном поле.

Заряженная частица влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции. Если скорость изменяется только по направлению, движение с постоянным по величине нормальным ускорением представляет собой равномерное движение по окружности a_н=v²/R. В случае когда частица влетает в поле не под прямым углом состовляющая силы лоренца в направлении В равна 0. Таким образом движение можно представить: перемещение вдоль В с постоянной скоростью и равномерным вращением в плоскости, перпендикулярной к вектору В. R=(mvsinα)/qB траектория движения представляет собой спираль.

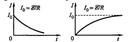Заряженная частица движется в магнитном поле вдоль линий магнитной индукции (угол a между векторами равен 0 или p). Сила Лоренца равна нулю. Магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

4. Эффект Холла

Эффект Холла: если металлическую пластинку, вдоль которой течет постоянный эл ток, поместить в перпенд. к ней магнитное поле, то возник разность потенциалов. U_н= , U_н=RbjB, R-постоянная холла, b-ширина пластинки, j-плотность тока, B-магнитная индукция. Явление Холла наблюдается не только в металлах но и в полу проводниках, причем по знаку эффекта можно определить о принадлежности полупроводника к n или p типу.

Дата добавления: 2015-10-21