Теорема Остроградского-Гаусса.

1. Поток вектора напряжённости.

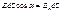Число линий напряженности, пронизывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора E. Число линий напряженности, пронизывающих элементарную площадку dS:

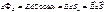Густота линий напряженности характеризует интенсивность электростатического поля. Элементарным потоком вектора напряженности через площадку dS называется:

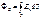Потоком вектора напряженности через поверхность S называется:

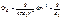Суммарный поток через пустую, замкнутую поверхность равен нулю. Поток вектора напряженности через сферическую поверхность радиуса r, охватывающую точечный заряд q, находящийся в ее центре

2. Теорема Остроградского-Гаусса.

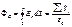Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов.

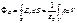3. Применение т. Остроградского-Гаусса для расчета электростатических полей.

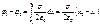
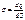· Поле равномерно заряженной бесконечной плоскости:

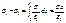· Поле двух бесконечных параллельных разноименно заряженных плоскостей с равными по абсолютному значению поверхностными плотностями зарядов:

· Поле равномерно заряженной сферической поверхности:

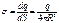
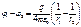Внутри сферы заряд отсутствует – напряженность поля внутри равно нулю. Вне сферы охватываемый гауссовой поверхностью заряд – равен полному заряду сферы.

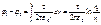Поле равномерно заряженного бесконечного цилиндра (нити):

---

Дата добавления: 2015-10-21