Задача 11

Ориентированный граф 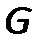задан матрицей смежности

1) Задать графически

2) Рассчитать полустепени вершин

3) Составить матрицы инцинденстности и достижимости

4) Определить тип связности орграфа, выделить компоненты связности

Решение:

Зададим орграф графически

Рассчитаем полустепени вершин:

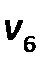
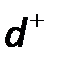
Составим матрицы инцинденстности и достижимости:

Обозначим дуги на нашем орграфе:

Строим матрицу инцидентности (столбцы соответствуют дугам, а строки вершинам)

Находим матрицу достижимости :

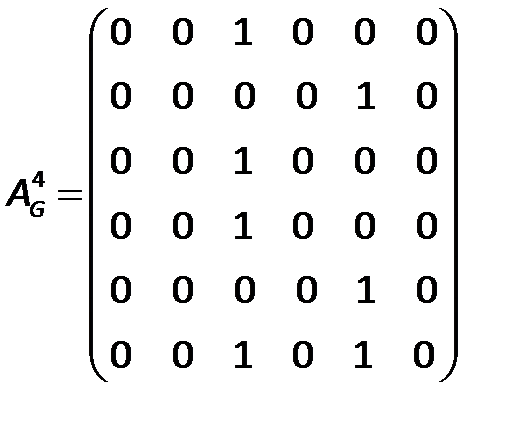
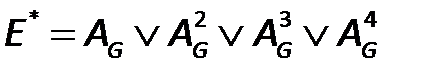
Таким образом, матрица достижимости имеет вид:

Определим тип связности орграфа:

Граф является слабо связным. Поскольку при учете направлений не каждая вершина оказывается достижима из любой, но при игнорировании направлений, получается связный граф.

Дата добавления: 2015-10-13