Задача 10

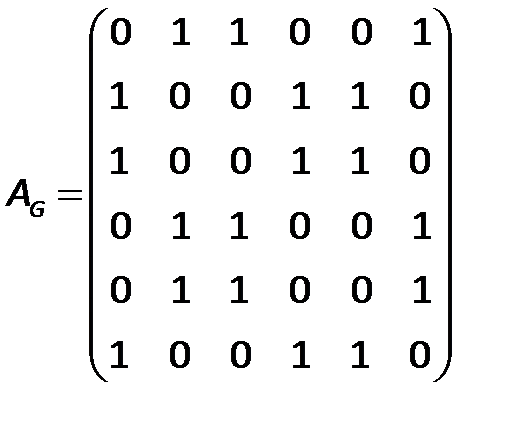
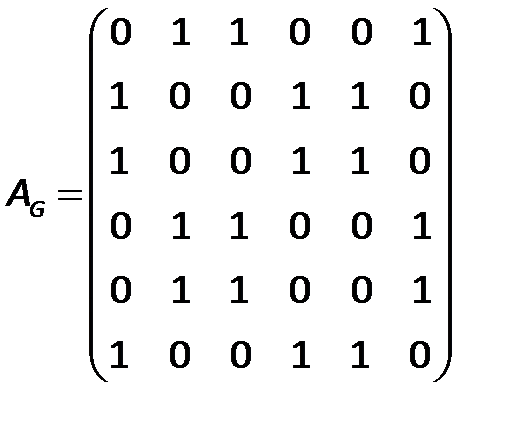
Граф 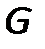задан матрицей смежности

1) Составить матрицу смежности дополнительного графа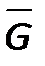

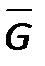2) Задать и графически и матрицами инцидентност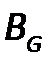и и . Рассчитать степени вершин графов.

3) Изоморфны ли графы и ?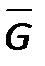

4) Являются ли графы и 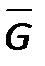связными? Определить количество компонент связности, найти мосты и точки сочленения.

5) Привести пример цикла в графе и цепи, не являющейся циклом в графе

6) Являются ли графы и 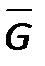а) планарными, б) двудольными, в) эйлеровыми, г) гамильтоновыми?

7) Привести пример остовного ациклического подграфа графа

Решение:

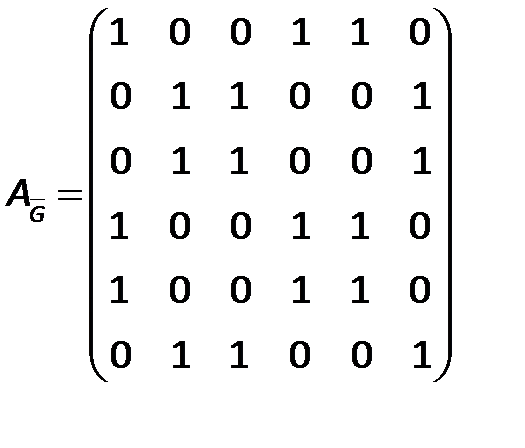
Составим матрицу смежности дополнительного графа

Для этого заменим в исходной матрице нули единицами, единицы нулями и получим матрицу смежности дополнительного графа

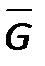Задать и графически:

Граф :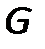

Граф :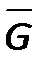

Запишем матрицы инцидентности для графов и :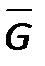

Ребра соответствуют столбцам матрицы, а вершины графа строкам

Рассчитаем степени вершин графов:

Учитываем, что при подсчете степени вершин, петля учитывается дважды.

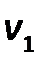
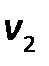
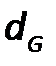
Проверка изоморфности графов и :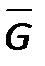

Графы изоморфны, так как из матрицы смежности графа можно получить матрицу смежности графа , путем перестановок строк:

Поменяв местами во второй матрице первую строку с последней, а также 4-ю и 5-ю со 2-й и 3-й соответственно, получим первую матрицу.

Проверка связности графов:

Граф 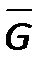не является связным, так как, например, не существует цепи, которая соединяла бы вершины с номерами 6 и 4.

Граф является связным, так как для любой пары вершин найдется цепь, соединяющая их.

Пример цикла в графе и цепи, не являющейся циклом в графе :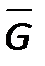

Например, следующий цикл в графе не является циклом в графе :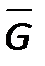

Графы и оба являются планарными, потомучто их можно изобразить на плоскости без пересечения ребер, то есть:

Граф :

Граф :

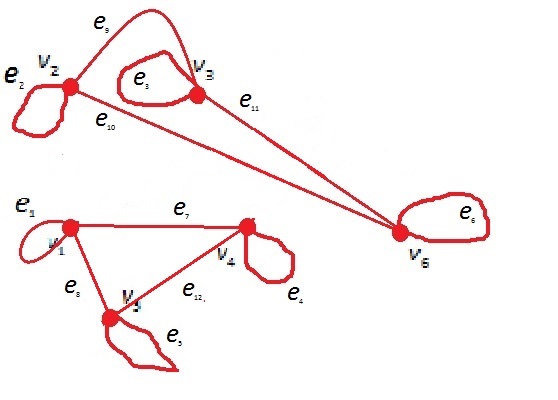
Графы и оба не являются двудольными, потомучто в каждом из них содержится цикл нечетной длины:

Граф :

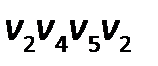
Граф :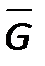

Графы и 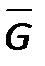оба не являются эйлеровыми:

Граф 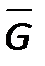: не является связным

Граф : все вершины имеют нечетную степень

Граф 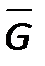не является гамильтоновым, так как не является связным

Граф является гамильтоновым, так как существует простой цикл 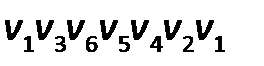который содержит все вершины графа ровно по одному разу.

Изобразим пример остовного ациклического подграфа графа :

Дата добавления: 2015-10-13