БИЛЕТ № 19

1. Число перестановок может быть рассчитано по формуле:

А) Р .	В)
Б) Р 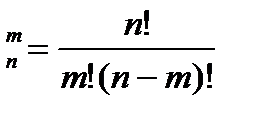;	Г) Р ;

2. Согласно свойству сочетаний:

А) ;	В) ;
Б) ;	Г) ;

3.	Противоположными называются:
А.	два единственно возможных и совместных события;
Б.	два равновозможных и совместных события;
В.	два равновозможных и несовместных события;
Г.	два единственно возможных и несовместных события.

4.	Классическое определение вероятности гласит:
А.	вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех равновозможных и несовместных событий;
Б.	вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и равновозможных событий;
В.	вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных, равновозможных и несовместных событий;
Г.	вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных событий.

5. Теорема сложения двух совместных событий может быть записана как:

А)	В)
Б)	Г)

6. Вероятность, найденную по формуле Байеса называют:

А) статистической;

Б) априорной;

В) апостериорной;

Г)безусловной.

7. Формула Бернулли записывается как:

А) ;

Б) ;

В) ;

Г) .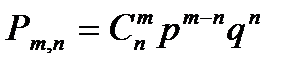

8. Дисперсия СВ, распределенной по гипергеометрическом закону определяется как:

А) 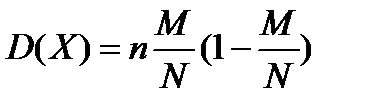;	В) ;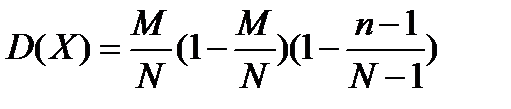
Б) 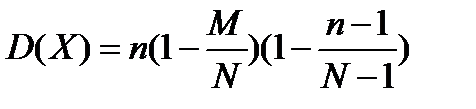;	Г) .

9. Математическое ожидание СВ, распределенной по закону Пуассона рассчитывается как:

А) ;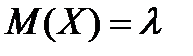

Б) ;

В) ;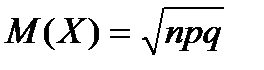

Г) .

10. Нормально распределенная СВ имеет плотность распределения, определяемую формулой:

А) ;	В) ;
Б) 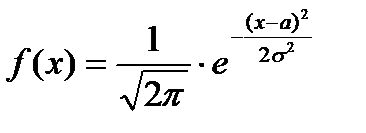;	Г) ;

11. Стандартная (нормированная) нормальная СВ имеет плотность распределения, определяемую формулой:

А) ;	В) ;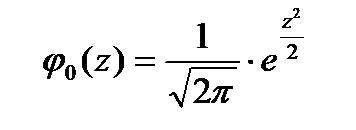
Б) ;	Г) .

12.	В узком смысле слова под законом больших чисел понимают
А.	совокупность теорем, в которых устанавливается факт приближения средних характеристик к некоторым постоянным величинам в результате большого числа наблюдений;
Б.	центральную предельную теорему Ляпунова;
В.	неравенство Маркова;
Г.	общий случай теоремы Чебышева.

Задача: вероятность сдать экзамен на право вождения автомобиля одинакова для всех слушателей курсов и равна 0,8. В группе 20 человек. Какому закону распределения будет подчиняться число слушателей, получивших права?

А) биномиальному;	В) равномерному;
Б) гипергеометрическому;	Г) закону распределения Пуассона.

14. Асимметрия характеризует:

А) скошенность ряда;	В) размерность ряда;
Б) вершинность ряда;	Г) вариацию ряда.

15. Формула простой дисперсии записывается как:

А)

Б)

В)

Г)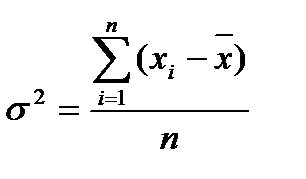

16.	Доверительная вероятность - это
А.	вероятность того, что доверительный интервал накроет неизвестный оцениваемый параметр генеральной совокупности
Б.	вероятность, которую можно признать достаточной для суждения о достоверности характеристик, полученных на основе генеральной совокупности
В.	вероятность, которая определяется исходя из предположения об обязательном осуществлении события
Г.	вероятность суммы двух событий А и В.

17. Различают следующие случайные ошибки выборки:

А) средняя (стандартная) ошибка;	В) возможная ошибка;
Б) предельная ошибка;	Г) средняя и предельная ошибки.

18. Необходимый объем выборки для оценки генеральной доли при собственно- случайном бесповторном отборе может быть найден как:

А) ;

Б) ;

В) ;

Г) ;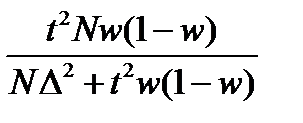

Дата добавления: 2015-10-13