БИЛЕТ № 17

1.	Перестановки - это
А.	соединения из n элементов по m в каждом, каждое из которых содержит m элементов, взятых из числа данных n элементов, и каждое из которых отличается друг от друга порядком расположения элементов;
Б.	соединения из n элементов по m в каждом, каждое из которых содержит m элементов, взятых из числа данных n элементов, и каждое из которых отличается друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения;
В.	соединения из n элементов по m в каждом, каждое из которых содержит m элементов, взятых из числа данных n элементов, и каждое из которых отличается друг от другу по крайне мере одним элементом;
Г.	соединения из n элементов, каждое из которых содержит все элементы, и которые отличаются друг от друга лишь порядком расположения элементов.

2.	Совместные события могут быть определены как:
А.	несколько событий называются совместными, если в результате опыта наступление одного из них исключает появление других;
Б.	несколько событий называются совместными, если в результате опыта наступление одного из них не исключает появление других;
В.	несколько событий называются совместными если в результате испытания хотя бы одно из них обязательно произойдет;
Г.	несколько событий называются совместными, если в результате испытания ни одно из них не имеет объективно большую возможность появления, чем другие.

3.	Вероятностью наступления события А называют отношение
А.	числа исходов (шансов), благоприятствующих противоположному событию, к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу;
Б.	числа исходов (шансов), благоприятствующих этому событию, к общему числу всех равновозможных несовместных элементарных исходов без благоприятных этому событию шансов (исходов);
В.	числа исходов (шансов), благоприятствующих этому событию, к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу;
Г.	числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.

4. Теорема сложения двух несовместных событий может быть записана как:

А)	В)
Б)	Г)

5. В коробке 6 красных и 4 зеленых карандаша. Один за другим извлекаются 2 карандаша, не возвращая уже извлеченные. Вероятность того, что оба карандаша будут зелеными может быть найдена как:

А) ;	В) ;
Б) 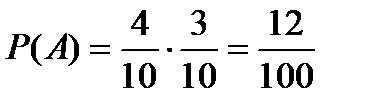;	Г) .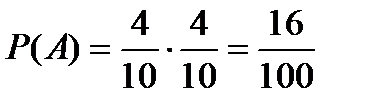

6. Формула Байеса может быть записана как:

А)	В)
Б)	Г)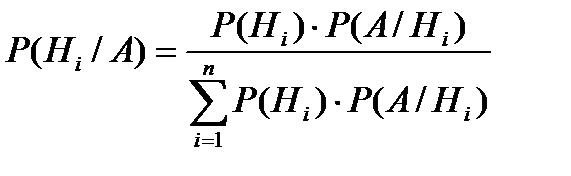

7.	Случайную величину называют дискретной если:
А.	множество ее значений конечно, но несчетно;
Б.	она может принять любое значение из некоторого конечного или бесконечного интервала;
В.	она может принять конкретное, заранее определенное значение из некоторого конечного или бесконечного интервала;
Г.	множество ее значений счетное.

.

8. Формула Бернулли записывается как:

А) ;

Б) ;

В) ;

Г) .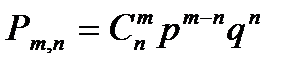

9. Математическое ожидание СВ, распределенной по гипергеометрическом закону:

А) ;

Б) ;

В) ;

Г) .

10. Распределение Пуассона называют также законом распределения:

А) частых событий;	В) зависимых событий;
Б) редких событий;	Г) совместных событий.

11. Согласно свойствам функции распределения F(x), вероятность того, что НСВ примет одно определенное значение равна::

А)единице;

Б) нулю;

В) бесконечности;

Г) минус бесконечности.

12. Вероятность заданного отклонения нормально распределенной СВ от ее математического ожидания на величину меньшую Δ равна:

А)	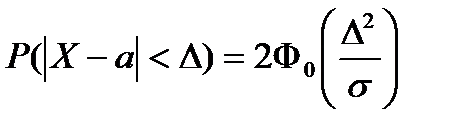В)
Б)	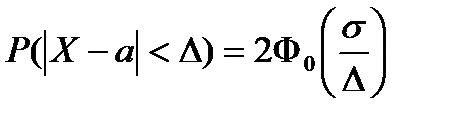Г)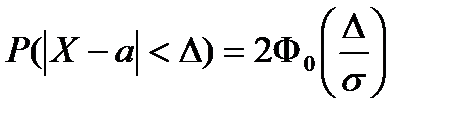

13. Теорема Чебышева имеет:

А) общий случай;	В) частный случай;
Б) классический случай;	Г) общий и частный случай.

Задача: в барабане книжной лотереи осталось 10 билетов, среди которых 2 выигрышные. Покупатель приобрел 3 билета. Какому закону распределения подчиняется число выигрышных билетов, доставшихся покупателю?

А) биномиальному;	В) равномерному;
Б) гипергеометрическому;	Г) закону распределения Пуассона.

15. Выбор оптимальной величины интервала для интервального ряда с равными интервалами осуществляется по:

А) абсолютной плотности	В) формуле Стэрджесса
Б) относительной плотности	Г) частости

16. Средняя арифметическая взвешенная рассчитывается как:

А) ;

Б) ;

В) ;

Г) .

17.	Оцениваемый параметр может иметь:
А.	две точечных оценки
Б.	только одну точечную оценку;
В.	множество точечных оценок;
Г.	три точечных оценки.

18. Ошибки репрезентативности возникают вследствие:

А) ошибок печати;	В) искажения сигналов в каналах связи;
Б) нарушения научных принципов отбора;	Г) ошибок в вычислении предельной ошибки выборки.

19. Необходимый объем выборки для оценки генеральной средней при собственно- случайном бесповторном отборе может быть найден как:

А) ;

Б) ;

В) ;

Г) ;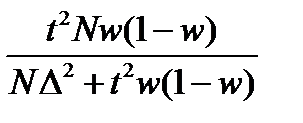

20. Критические области бывают:

А) только односторонними;	В) только трехсторонними;
Б) только двухсторонними;	Г)одно- или двухсторонними.

Дата добавления: 2015-10-13