БИЛЕТ № 18

1. Число размещений может быть рассчитано по формуле:

А) A 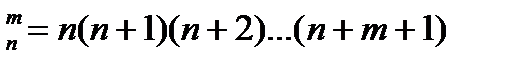;	В) A ;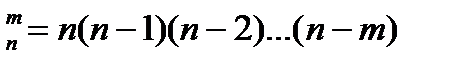
Б) A 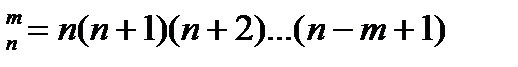;	Г) A .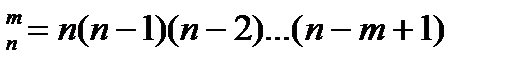

2. Директор компании рассматривает заявления о приеме на работу 5 выпускников университета. В компании имеются три одинаковых вакансии. Сколькими способами директор может заполнить эти вакансии? Для решения задачи нужно использовать:

А) формулу сочетаний;	В) формулу размещений;
Б) формулу перестановок;	Г) формулу перестановок с повторениями.

3.	Единственно возможные события могут быть определены как:
А.	несколько событий называются единственно возможными, если в результате опыта наступление одного из них исключает появление других;
Б.	несколько событий называются единственно возможными, если в результате опыта наступление одного из них не исключает появление других;
В.	несколько событий называются единственно возможными если в результате испытания хотя бы одно из них обязательно произойдет
Г.	несколько событий называются единственно возможными, если в результате испытания ни одно из них не имеет объективно большую вероятность появления, чем другие.

4.	Теорема сложения несовместных событий утверждает, что:
А.	вероятность суммы двух несовместных событий равна сумме вероятностей этих событий;
Б.	вероятность суммы двух несовместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления;
В.	вероятность суммы двух несовместных событий равна разности вероятностей этих событий;
Г.	вероятность суммы двух несовместных событий равна сумме вероятностей этих событий плюс вероятность их совместного наступления.

5.	Формула Байеса позволяет:
А.	переоценить полную вероятность события А;
Б.	вычислить полную вероятность события А;
В.	переоценить условные вероятности события А, после того, как становится известным результат испытания, в итоге которого появилось событие А;
Г.	переоценить вероятности гипотез, после того, как становится известным результат испытания, в итоге которого появилось событие А.

Дата добавления: 2015-10-13