БИЛЕТ № 16

1.	Размещения - это
А.	соединения из n элементов по m в каждом, каждое из которых содержит m элементов, взятых из числа данных n элементов, и каждое из которых отличается друг от друга порядком расположения элементов;
Б.	соединения из n элементов по m в каждом, каждое из которых содержит m элементов, взятых из числа данных n элементов, и каждое из которых отличается друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения;
В.	соединения из n элементов по m в каждом, каждое из которых содержит m элементов, взятых из числа данных n элементов, и каждое из которых отличается друг от друга по крайне мере одним элементом;
Г.	соединения из n элементов, каждое из которых содержит все элементы, и которые отличаются друг от друга лишь порядком расположения элементов.

2.	Несовместные события могут быть определены как:
А.	несколько событий называются несовместными, если в результате опыта наступление одного из них исключает появление других;
Б.	несколько событий называются несовместными, если в результате опыта наступление одного из них не исключает появление других;
В.	несколько событий называются несовместными если в результате испытания хотя бы одно из них обязательно произойдет;
Г.	несколько событий называются несовместными, если в результате испытания ни одно из них не имеет объективно большую вероятность появления, чем другие.

3.	Классическое определение вероятности утверждает:
А.	вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех равновозможных и несовместных событий;
Б.	вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и равновозможных событий;
В.	вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных, равновозможных и несовместных событий
Г.	вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных событий.

4.	Теорема сложения совместных событий утверждает, что:
А.	вероятность суммы двух совместных событий равна сумме вероятностей этих событий;
Б.	вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления;
В.	вероятность суммы двух совместных событий равна разности вероятностей этих событий;
Г.	вероятность суммы двух совместных событий равна сумме вероятностей этих событий плюс вероятность их совместного наступления.

.

5.Формула полной вероятности может быть записана как:

А)	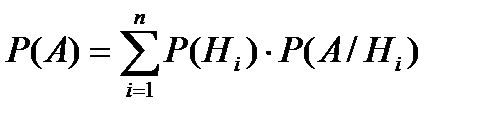В)
Б)	Г)

6.	Случайная величина – это
А.	величина, которая в результате опыта (испытания, эксперимента) принимает одно из своих возможных значений, причем заранее неизвестно какое именно;
Б.	величина, которая в результате опыта (испытания, эксперимента) принимает одно из своих возможных значений, причем заранее известно какое именно;
В.	величина, которая в результате опыта (испытания, эксперимента) принимает несколько из своих возможных значений, причем заранее неизвестно какие именно;
Г.	величина, которая в результате опыта (испытания, эксперимента) принимает несколько из своих возможных значений, причем заранее известно какие именно.

7. Дисперсия биномиального распределения рассчитывается как:

А) ;

Б) ;

В) ;

Г) .

6. Математическое ожидание биномиального распределения рассчитывается как:

А) ;

Б) ;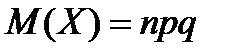

В) ;

Г) .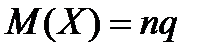

8.	Распределение Пуассона - это
А.	распределение вероятностей времени до первого наступления события;
Б.	распределение вероятностей числа наступлений события в течение промежутка времени;
В.	распределение вероятностей числа испытаний до первого появления события;
Г.	распределение вероятностей числа наступлений события в n зависимых испытаниях.

9.	Плотностью вероятности (плотностью распределения или просто плотностью) непрерывной случайной величины называется
А.	определенный интеграл функции распределения этой случайной величины;
Б.	интегральный закон распределения случайной величины;
В.	производная функции распределения этой случайной величины
Г.	площадь фигуры, ограниченной кривой распределения и точки, лежащей правее точки Х

10. Вероятность попадания нормально распределенной СВ в заданный интервал вычисляется:

А) 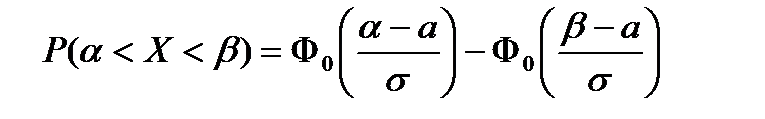;	В) ;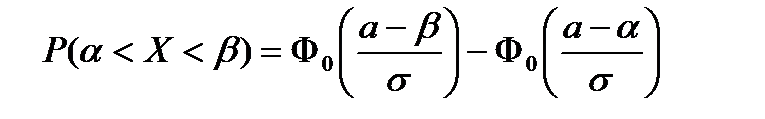
Б) 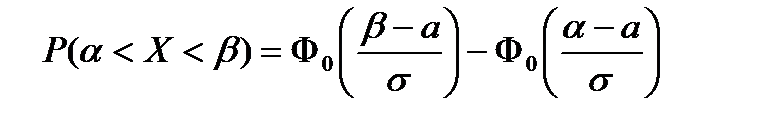;	Г) .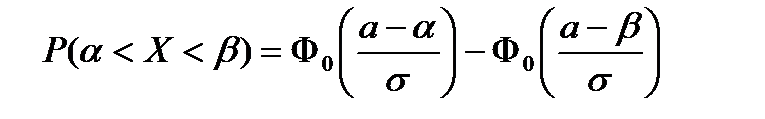

11.	В узком смысле слова под законом больших чисел понимают:
А.	совокупность теорем, в которых устанавливается факт приближения средних характеристик к некоторым постоянным величинам в результате большого числа наблюдений;
Б.	центральную предельную теорему Ляпунова;
В.	неравенство Маркова;
Г.	общий случай теоремы Чебышева.

Задача: вероятность сдать экзамен по математической статистике одинакова для всех студентов группы и равна 0,7. В группе 20 человек. Какому закону распределения будет подчиняться число студентов, сдавших экзамен?

А) биномиальному;	В) равномерному;
Б) гипергеометрическому;	Г) закону распределения Пуассона.

13. Абсолютная плотность - это:

А) отношение частоты интервала к величине интервала;	В) отношение частости интервала к величине интервала;
Б) накопленная частость;	Г) накопленная частота.

14. Коэффициент асимметрии рассчитывается как:

А) ;

Б) ;

В) ;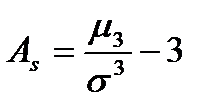

Г) .

15. Точечной оценкой генеральной дисперсии при объеме выборке 30 является:

А) ;

Б) ;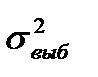

В) ;

Г) .

16.	Сущность выборочного метода состоит в том, что:
А.	для изучения вместо всей совокупности элементов берётся лишь некоторая их часть, отобранная по определённым правилам;
Б.	для исследования все элементы изучаемой совокупности группируются по определённым правилам;
В.	элементы изучаемой совокупности отбираются через определённый интервал;
Г.	сначала обследуются все элементы изучаемой совокупности, а затем по определённым правилам отбирается их некоторая часть.

17. Малые выборки описываются законом распределения вероятностей:

А) нормальным В) 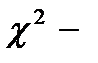Пирсона

Б) t ‑ Стьюдента Г) F- Фишера

18. Предельная ошибка выборки равна:

А) сумме стандартной ошибки и величины кратности ошибки;

Б) частному от деления величины кратности ошибки и стандартной ошибки;

В) разности стандартной ошибки и величины кратности ошибки;

Г) t-кратному числу стандартных ошибок выборки.

z-кратному числу средних ошибок выборки

19. Типическая выборка основана на

А) использовании таблиц случайных чисел;	В) жребия;
Б) отборе элементов из списков через определенный интервал;	Г) разбиении генеральной совокупности на группы по некоторому общему признаку.

20. Статистическая гипотеза называется непараметрической, если в ней сформулированы предположения относительно:

А) вида закона распределения;

Б) неизвестных значений параметров распределения определенного вида;

В) уровня значимости;

Г) известных значений параметров распределения определенного вида.

Дата добавления: 2015-10-13