
|
Читайте также: |
Используя выбранные точки можно преобразовать нелинейные ограничения и нелинейную ЦФ к кусочно-линейному виду. К ограничениям также добавятся ограничения, обеспечивающие свойство весов смежных точек. В итоге получим задачу линейного программирования.
Таблица 3.9. – Целевая функция для сепарабельного симплекс-метода
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | X11 | x12 | x13 | x14 | |
| Y= | 266/729 | 524/729 | 86/81 |
| x15 | x16 | x17 | x18 | x19 | x20 | x21 | x22 | x23 | x24 | x25 |
| 1016/729 | 1250/729 | 164/81 | 1694/729 | 1904/729 | 26/9 |
| x26 | x27 | x28 | x29 | x30 | x31 | x32 | x33 | x34 | x35 | x36 |
| -2/729 | -8/729 | -2/81 | -32/729 | -50/729 |
| x37 | x38 | x39 | x40 | x41 | x42 | x43 | x44 | x45 | x46 | x47 |
| -8/81 | -98/729 | -128/729 | -2/9 | 2/9 | 128/729 | 98/729 | 8/81 | 50/729 | 32/729 | 2/81 |
| x48 | x49 | x50 | x51 | x52 | СЧ |
| 8/729 | 2/729 |
Таблица 3.10. – Ограничения для сепарабельного симплекс-метода
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | x16 | x17 |
| 2/9 | 4/9 | 2/3 | 8/9 | 10/9 | 4/3 | |||||||||||
| 1/27 | 2/27 | 1/9 | 4/27 | 5/27 | 2/9 | |||||||||||
| -1/27 | -2/27 | -1/9 | -4/27 | -5/27 | -2/9 |
| x18 | x19 | x20 | x21 | x22 | x23 | x24 | x25 | x26 | x27 | x28 | x29 | x30 | x31 | x32 |
| 14/9 | 16/9 | |||||||||||||
| 7/27 | 8/27 | 1/3 | -1/27 | |||||||||||
| -7/27 | -8/27 | -1/3 |
| x33 | x34 | x35 | x36 | x37 | x38 | x39 | x40 | x41 | x42 | x43 | x44 | x45 |
| -2/27 | -1/9 | -4/27 | -5/27 | -2/9 | -7/27 | -8/27 | -1/3 | |||||
| 1/3 | 8/27 | 7/27 | 2/9 | 5/27 |
| x46 | x47 | x48 | x49 | x50 | x51 | x52 | ||
| = | ||||||||
| = | ||||||||
| = | ||||||||
| = | ||||||||
| = | ||||||||
| = | ||||||||
| = | ||||||||
| = | ||||||||
| 4/27 | 1/9 | 2/27 | 1/27 | = |
Введем необходимые свободные и искусственные переменные и выразим все ограничения в форме Таккера. Теперь решим задачу линейного программирования: минимизировать ЦФ вида:
Y = x53+x54 → max
Сепарабельный симплексный алгоритм аналогичен обычному симплекс методу, за исключением необходимости соблюдения правила ограниченного ввода в базис, суть которого заключается в том, что оптимальное решение, полученное с использованием аппроксимирующей модели, содержит либо один вес  , либо два соседних
, либо два соседних 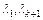 .
.
Оптимизируем искусственную целевую функцию с соблюдением этого правила. Получив оптимальное решение, осуществим стандартную процедуру перехода от искусственной целевой функции к исходной. Теперь решим полученную задачу с помощью сепарабельного симплекс-метода. Все этапы решения приведены в приложении В. Полученные результаты удовлетворяют ограничениям.
Ответ: Y = 26/9, X = (0; 2/3; 0).
Дата добавления: 2015-09-07; просмотров: 115 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение задачи методом Била | | | Переход от прямой задачи к двойственной |