Решение задачи методом ветвей и границ

.

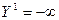Задача №1 - исходная задача со снятым требованием целочисленности. Перепишем решение из таблицы 1.12.

Таблица 2.56

БП	СЧ	X1	X2	X3	X4	X5	X6	X7	X8
X4	7/2			-3/4		1/2		1/2	-3/4
X6	229/8			21/16		23/8		29/8	-99/16
X2	5/8			13/16		-1/8		-3/8	5/16
X1	35/8			11/16		1/8		3/8	-13/16
Y	-109/8			139/16		9/8		11/8	3/16

Решение данной задачи не удовлетворяет требованиям целочисленности, поэтому необходимо простроить две порождённые задачи. Для образования порожденных задач выберем переменную Х4.

Задача №2 - к исходным данным задачи №1 добавляется ограничение Х4>=4.

Выразим допустимый базис в форме Таккера:

x₅=3-(-2x₁+2x₂-2x₃+3x₄)

x₆=-2-(-3x₁+0x₂+3x₃-5x₄)

x₇=-11-(-1x₁-5x₂-4x₃-1x₄)

x₈=-10-(-2x₁-2x₂-3x₃+0x₄)

x₉=-4-(0x₁+0x₂+0x₃-1x₄)

Целевая функция в форме Таккера:

Y=0-(4x₁+5x₂+17x₃-2x₄)

Таблица 2.57

БП	СЧ	X1	X2	X3	X4	X5	X6	X7	X8	X9
X5		-2		-2
X6	-2	-3			-5
X7	-11	-1	-5	-4	-1
X8	-10	-2	-2	-3
X9	-4				-1
Y					-2

Используем двойственный симплекс-метод. Вводим в базис X2, выводим из базиса X7.

Таблица 2.58

БП	СЧ	X1	X2	X3	X4	X5	X6	X7	X8	X9
X5	-7/5	-12/5		-18/5	13/5			2/5
X6	-2	-3			-5
X2	11/5	1/5		4/5	1/5			-1/5
X8	-28/5	-8/5		-7/5	2/5			-2/5
X9	-4				-1
Y	-11				-3

Используем двойственный симплекс-метод. Вводим в базис X1, выводим из базиса X8.

Таблица 2.59

БП	СЧ	X1	X2	X3	X4	X5	X6	X7	X8	X9
X5				-3/2					-3/2
X6	17/2			45/8	-23/4			3/4	-15/8
X2	3/2			5/8	1/4			-1/4	1/8
X1	7/2			7/8	-1/4			1/4	-5/8
X9	-4				-1
Y	-43/2			83/8	-9/4			1/4	15/8

Используем двойственный симплекс-метод. Вводим в базис X4, выводим из базиса X9.

Таблица 2.60

БП	СЧ	X1	X2	X3	X4	X5	X6	X7	X8	X9
X5	-1			-3/2					-3/2
X6	63/2			45/8				3/4	-15/8	-23/4
X2	1/2			5/8				-1/4	1/8	1/4
X1	9/2			7/8				1/4	-5/8	-1/4
X4										-1
Y	-25/2			83/8				1/4	15/8	-9/4

Используем двойственный симплекс-метод. Вводим в базис X8, выводим из базиса X5.

Таблица 2.61

БП	СЧ	X1	X2	X3	X4	X5	X6	X7	X8	X9
X8	2/3					-2/3		-2/3		-4/3
X6	131/4			15/2		-5/4		-1/2		-33/4
X2	5/12			2/4		1/12		-1/6		5/12
X1	59/12			3/2		-5/12		-1/6		-13/12
X4										-1
Y	-55/4			17/2		5/4		3/2		1/4

Решение задачи удовлетворяет требованию целочисленности для переменной х₄, и значение целевой функции больше, чем найденное до этого оптимально 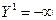. На данной итерации найдено новое оптимально целочисленное решение.

Задача №3 - к исходным данным задачи №1 добавляется ограничение Х4<=3.

Выразим допустимый базис в форме Таккера:

x₅=3-(-2x₁+2x₂-2x₃+3x₄)

x₆=-2-(-3x₁+0x₂+3x₃-5x₄)

x₇=-11-(-1x₁-5x₂-4x₃-1x₄)

x₈=-10-(-2x₁-2x₂-3x₃+0x₄)

x₉=3-(0x₁+0x₂+0x₃+1x₄)

Целевая функция в форме Таккера:

Y=0-(4x₁+5x₂+17x₃-2x₄)

Таблица 2.62

БП	СЧ	X1	X2	X3	X4	X5	X6	X7	X8	X9
X5		-2		-2
X6	-2	-3			-5
X7	-11	-1	-5	-4	-1
X8	-10	-2	-2	-3
X9
Y					-2

Используем двойственный симплекс-метод. Вводим в базис X2, выводим из базиса X7.

Таблица 2.63

БП	СЧ	X1	X2	X3	X4	X5	X6	X7	X8	X9
X5	-7/5	-12/5		-18/5	13/5			2/5
X6	-2	-3			-5
X2	11/5	1/5		4/5	1/5			-1/5
X8	-28/5	-8/5		-7/5	2/5			-2/5
X9
Y	-11				-3

Используем двойственный симплекс-метод. Вводим в базис X1, выводим из базиса X8.

Таблица 2.64

БП	СЧ	X1	X2	X3	X4	X5	X6	X7	X8	X9
X5				-3/2					-3/2
X6	17/2			45/8	-23/4			3/4	-15/8
X2	3/2			5/8	1/4			-1/4	1/8
X1	7/2			7/8	-1/4			1/4	-5/8
X9
Y	-43/2			83/8	-9/4			1/4	15/8

Используем обычный симплекс-метод. Вводим в базис X4, выводим из базиса X9.

Таблица 2.64

БП	СЧ	X1	X2	X3	X4	X5	X6	X7	X8	X9
X5				-3/2					-3/2	-2
X6	103/4			45/8				3/4	-15/8	23/4
X2	3/4			5/8				-1/4	1/8	-1/4
X1	17/4			7/8				1/4	-5/8	1/4
X4
Y	-59/4			83/8				1/4	15/8	9/4

Остановка: Решение задачи удовлетворяет требованию целочисленности для переменной х₄, но значение целевой функции не больше, чем найденное до этого.

Список задач пуст. Блок-схема решения задачи представлена на рисунке 2.2.

Ответ: Y=-55/4, X=(59/12;5/12;0;4;0;131/4;0;2/3;0).

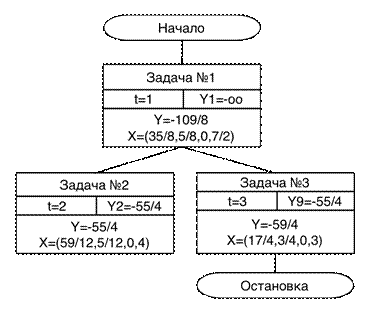
Рисунок 2.2 - Схема решения частично целочисленной задачи методом ветвей и границ.

Дата добавления: 2015-09-07