Момент инерции

Момент инерции тела сравнительно простой формы может быть определен путем вычислений. Рассмотрим простейший случай - вращение тела по окружности в случае, когда размеры тела пренебрежимо малы по сравнению с радиусом окружности (тело – материальная точка). Если тело закреплено на расстоянии R от неподвижной оси, то под действием силы 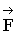, направленной по касательной к окружности и перпендикулярно оси вращения, оно приобретает тангенциальное ускорение

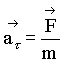(3.2)

так как за очень малый промежуток времени движение тела по окружности можно считать прямолинейным.

С другой стороны, рассматривая движение тела как вращательное, угловое ускорение его движения можно определить из основного уравнения динамики вращательного движения:

Из уравнений (2.1) и (3.2) получаем выражение для момента инерции тела:

Выражая тангенциальное ускорение через угловое ускорение и радиус вращения 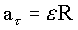, получим:

(3.3)

Итак, момент инерции тела, вращающегося по окружности радиуса R, большого по сравнению с размерами тела, равен произведению массы тела на квадрат расстояния от него до оси вращения.

Из уравнения (3.3) единица момента инерции в СИ будет: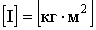

Полученный результат (3.3) позволяет решить задачу о нахождении момента инерции тела произвольной формы относительно любой оси вращения. Для этого необходимо мысленно разбить это тело на очень малые части, найти произведение массы каждой части на квадрат расстояния от нее до оси вращения и все эти произведения сложить. Эту операцию можно произвести сравнительно просто для таких тел, как обруч, тонкостенный цилиндр и т. д. Все точки обруча находятся на одинаковом расстоянии от оси вращения, проходящей через его центр перпендикулярно плоскости обруча.

Для таких тел как шар, цилиндр и многих других, у которых точки находятся на различных расстояниях от оси вращения, расчет момента инерции более сложен и производится методом высшей математики, называемым интегрированием.

Момент инерции тела человека, стоящего с прижатыми к туловищу руками относительно вертикальной оси, проходящей через его центр масс, равен примерно 1,2 кгм². Разведение в стороны рук и ног увеличивает момент инерции человека относительно той же оси почти в семь раз.

В таблице 3.1 приводятся моменты инерции некоторых тел относительно указанных осей.

Таблица 3.1.

Тело	Ось вращения проходит	Момент инерции
Тонкий стержень	Перпендикулярно стержню через его середину
Обруч (тонкостенный цилиндр)	Перпендикулярно плоскости кольца через его центр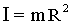
Диск (цилиндр)	Перпендикулярно плоскости диска через его центр
Плоский диск	Через цент диска вдоль его диаметра
Шар	Ось проходит через центр шара

Дата добавления: 2015-09-05