Наиболее часто нам будут встречаться дискретные случайные величины и их числовые характеристики

Дискретная случайная величина (ДСВ) может принимать конечное или бесконечное счетное число значений.

Законом распределения ДСВ называется соотношение между ее возможными значениями и их вероятностями (т. е. вероятностями, с которыми случайная величина принимает эти возможные значения).

Закон распределения может быть задан формулой (формулы Бернулли, Пуассона и др.), таблицей или графиком, а также функцией распределения.

Функцией распределения случайной величины называется функция

,

определяющая вероятность того, что случайная величина примет значение, меньшее .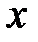

Свойства функции распределения:

а) функция распределения принимает значения только из отрезка [0,1]:

0 ≤ F(x) ≤ 1;

б) F(x) – неубывающая функция, т.е. если x₂ > x₁, то F(x₂) > F(x₁);

в) F(- ∞) = 0; F(+ ∞) = 1;

г) вероятность того, что случайная величина примет значение из

интервала (причем ), равна:

;

д) F(x) непрерывна слева, т. е. F(x) = F(x – 0)

Закон распределения дискретной случайной величины может быть представлен в виде многоугольника распределения – фигуры, состоящей из точек , соединенных отрезками (рис. 1.3).

Рис. 2. Многоугольники унимодального (а), полимодального (б) и антимодального (в) распределений

Дата добавления: 2015-09-06