Противоположностью по отношению к достоверному событию является событие невозможное.

Невозможным называется событие, которое при реализации определенного комплекса условий произойти не может.

Пример: два попадания в цель при единичном выстреле по цели и т. д.

Невозможному событию приписывается вероятность, равная 0.

Таким образом, мы установили меру вероятности, диапазон ее возможных значений. Вероятность появления случайного события всегда больше нуля и меньше единицы, что символически записывается следующим образом:

0< Р(А) < 1,

где: А — случайное событие;

Р (А) вероятность появления события А.

Определим понятие «полная группа событий».

События образуют полную группу событий, если при реализации определенного комплекса условий хотя бы одно из них появится непременно.

Пример: промах и попадание в цель при единичном выстреле по цели и т. д.

Вероятность появления какого-либо события из полной группы событий при реализации определенного комплекса условий равна 1.

События называются несовместными, если никакие два из них при реализации определенного комплекса условий не могут появиться совместно.

Пример: здоровый человек, находящийся в контакте с инфекционным больным, не может одновременно заболеть и не заболеть, или заболеть и оказаться носителем инфекции и заболеть и не оказаться носителем инфекции.

Два несовместных события, образующих полную группу несовместных событий, называются противоположными событиями.

Обозначим событие, противоположное основному, той же буквой с. чертой сверху. Например, события «попадание в цель» (А) и «промах» (А) при одиночном выстреле по цели или события «заболеть» (А) и «не заболеть» (А) при контакте с инфекционным больным.

Несколько событий называются равновозможными, если при реализации определенного комплекса условий по условиям симметрии есть основание считать, что ни одно из них не является объективно более возможным, чем другие.

Пример: выбор белого или черного шара из урны, в которой находится одинаковое число черных й белых шаров.

Когда в группе событий события являются одновременно несовместными и равновозможными и образуют полную группу событий, то события называются шансами или случаями, и тогда мы имеем дело со схемой шансов, случаев.

Если какой-либо опыт сводится к схеме случаев, то вероятность события можно приравнять частоте благоприятных случаев, т. е. случаев, в которых произошло данное событие.

Если обозначить через m число случаев, в которых появилось событие А, а через n — общее число случаев, в которых реализовывался определенный комплекс условий, то вероятность появления события А вычисляется по формуле:

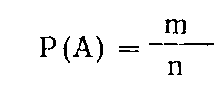
При этом для невозможного события т = 0 и Р(А)=0, для достоверного — m = n и Р(А) = 1, для случайного — m<n и 0<Р(А) <1.

Эта формула пригодна тогда и только тогда, когда опыт сводится к схеме случаев, т. е. обладает симметрией возможных исходов. Большинство же интересующих нас опытов и наблюдений не сводятся к схеме случаев.

Дата добавления: 2015-09-06