Погрешность метода

Оценим погрешность при вычислении первой производной при помощи соотношения:

где O(h) есть погрешность метода. В данном случае под погрешностью метода понимается абсолютная величина разности

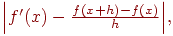
которая составляет O(h) (более точно

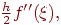
где ).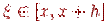

Если же взять другой метод вычисления производной

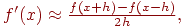
то получим, что его погрешность составляет O(h²), это оказывается существенным при малых h. Однако уменьшать h до бесконечности не имеет смысла, что видно из следующего примера. Реальная погрешность при вычислении первой производной будет

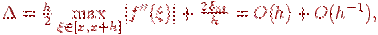
поскольку абсолютная погрешность вычисления значения функции за счет машинного округления не превосходит

В этом случае можно найти оптимальный шаг h. Будем считать полную погрешность в вычислении производной Δ функцией шага h. Отыщем минимум этой функции. Приравняв производную Δ'_h(h) к нулю, получим оптимальный шаг численного дифференцирования

Выбирать значение h меньше оптимального не имеет смысла, так как при дальнейшем уменьшении шага суммарная погрешность начинает расти из-за возрастания вклада ошибок округления.

Задание:

1. Внимательно изучите предложенный Вам материал и составьте конспект.

2. Ответьте на следующие вопросы:

2.1. Дайте определение числу.

2.2. Дайте определение вещественному числу.

2.3. Как хранятся числа в памяти компьютера?

2.4. Как хранятся целые числа без знака в памяти компьютера?

2.5. Как хранятся целые числа со знаком в памяти компьютера?

2.6. Как хранятся отрицательные целые числа без знака в памяти компьютера?

2.7. Какой формат называется форматом с плавающей точкой и как представляется вещественное число R?

2.8. Что такое мантисса числа и как она представляется в памяти компьютера?

2.9. Что такое машинный порядок?

2.10. Что необходимо сделать для записи внутреннего представления вещественного числа?

2.11. Когда происходит прерывание программы при вычислениях с вещественными числами?

2.12. Что называют погрешностью машинных округлений?

2.13. Каковы специфические особенности вычислительной математики?

2.14. Перечислите причины погрешностей машинных вычислений.

Список рекомендуемой литературы:

1. Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad, стр. 10-14

2. http://www.intuit.ru/department/calculate/calcmathbase/

3. http://www.knigafund.ru/books/38194

Дата добавления: 2015-09-06