Специфические особенности вычислительной математики
Вычислительная математика отличается от других математических дисциплин и обладает специфическими особенностями.
- Вычислительная математика имеет дело не только с непрерывными, но и с дискретными объектами. Так, вместо отрезка прямой часто рассматривается система точек
 , вместо непрерывной функции f(x) — табличная функция
, вместо непрерывной функции f(x) — табличная функция 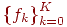 , вместо первой производной — ее разностная аппроксимация, например,
, вместо первой производной — ее разностная аппроксимация, например,
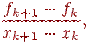

Такие замены, естественно, порождают погрешности метода.
- В машинных вычислениях присутствуют числа с ограниченным количеством знаков после запятой из-за конечности длины мантиссы при представлении действительного числа в памяти ЭВМ. Другими словами, в вычислениях присутствует машинная погрешность (округления)
 . Это приводит к вычислительным эффектам, неизвестным, например, в классической теории обыкновенных дифференциальных уравнений, уравнений математической физики или в математическом анализе.
. Это приводит к вычислительным эффектам, неизвестным, например, в классической теории обыкновенных дифференциальных уравнений, уравнений математической физики или в математическом анализе. - В вычислительной практике большое значение имеет обусловленность задачи, т.е. чувствительность ее решения к малым изменениям входных данных.
- В отличие от "классической" математики выбор вычислительного алгоритма влияет на результаты вычислений.
- Существенная черта численного метода — экономичность вычислительного алгоритма, т.е. минимизация числа элементарных операций при выполнении его на ЭВМ.
- Погрешности при численном решении задач делятся на две категории — неустранимые и устранимые. К первым относят погрешности, связанные с построением математической модели объекта и приближенным заданием входных данных, ко вторым — погрешности метода решения задачи и ошибки округления, которые являются источниками малых возмущений, вносимых в решение задачи.
Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.
Дата добавления: 2015-09-06; просмотров: 109 | Нарушение авторских прав
Читайте в этой же книге: Влияние выбора вычислительного алгоритма на результаты вычислений | Экономичность вычислительного метода | Погрешность метода |
mybiblioteka.su - 2015-2025 год. (0.006 сек.)

 , вместо непрерывной функции f(x) — табличная функция
, вместо непрерывной функции f(x) — табличная функция 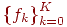 , вместо первой производной — ее разностная аппроксимация, например,
, вместо первой производной — ее разностная аппроксимация, например, 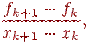

 . Это приводит к вычислительным эффектам, неизвестным, например, в классической теории обыкновенных дифференциальных уравнений, уравнений математической физики или в математическом анализе.
. Это приводит к вычислительным эффектам, неизвестным, например, в классической теории обыкновенных дифференциальных уравнений, уравнений математической физики или в математическом анализе.