
|
Читайте также: |
Теория звука в ее классической форме строится на основе законов движения газов с учетом особенности колебательных движений с малой амплитудой.
Движение газов подчиняется законам аэродинамики. Уравнения в общей форме нелинейны и трудно поддаются решению. Поэтому делают ряд упрощающих предположений.
Аэродинамика идеального газа, лишенного вязкости, применяющая при решении задач, связанных с движением газов, в частности воздуха. Однако без учета вязкости невозможно вычислить сопротивление газа движению тела.
При скорости движения, меньших, чем скорости звука, можно пренебрегать сжимаемостью газов. Аэродинамика несжимаемого газа применима в известной степени. Кажущаяся несжимаемость газов является следствием того, что при скоростях меньших скорости звука, всякие изменения давления, вызванные движением тела, распространяются в форме звуковой волны и опережают движущееся тело. В пределах ограниченных размеров движущегося тела деформация газа остается неизменной, что эквивалентно несжимаемости.
При скоростях, приближающихся к скорости звука и больших, газы нельзя считать несжимаемыми и необходимо учитывать влияние теплопроводности при быстро протекающих процессах. Аэродинамика сжимаемого газа — газодинамика.
При строгом решении задачи о колебательных движениях в сплошны средах их необходимо считать сжимаемыми. При таких движениях в телах, имеющих достаточно большую протяженность, возникают волны, которые передают возникающие деформации и давление от места их возникновения во все стороны с конечной скоростью (скоростью звука).
Основные вопросы акустики разрешаются в предположении малых амплитуд колебаний, но с учетом сжимаемости среды.
Акустика — газодинамика малых амплитуд.
Большинство вопросов излучения и распространения звука решается при помощи волнового уравнения. Это уравнение получается из уравнения движения идеального газа и уравнения неразрывности среды и уравнения состояния.
Полная система уравнений акустики.
Основывается на втором законе Ньютона (F = m·a).

где x — координата; ξ — ρмещение
Звуковые волны распространяются в 3-х измерениях. Они являются продольными волнами. Молекулы воздуха движутся в направлении распространения волн, так что происходит чередование сжатий и разряжений. Восстанавливающей силой, необходимой для существования волнового движения, является сопротивление, которое газ оказывает сжатию.
Плоские звуковые волны — волны, распространяющиеся в пространстве в одном направлении, области сжатия и разряжения, которых, располагаются в плоскостях, перпендикулярных к направлению распространению волн.
Основные положения.
 Рассмотрим воздух в прямой трубе неизменимого поперечного сечения S.
Рассмотрим воздух в прямой трубе неизменимого поперечного сечения S.
Когда звуковая волна распространяется по трубе плоскости х1 и х2 будут смещаться из положения равновесия взад и вперед по трубе х1 + ξ(υ1) и х2 + ξ(υ2). Каждая молекула газа, находящаяся первоначально на расстоянии х от начала переместится на расстояние ξ. έто смещение зависит от времени t и от положения молекулы х.
ξ (x,t).
Т.к. молекула участвует в тепловом движении (броуновское движение), то ξ (x,t) представляет собой среднее смещение ξ..
 Обозначим ρ 0 и р0 плотность и давление газа в состояние равновесия. Действительная плотность в точке Х в момент времени t – ρ(x,t).
Обозначим ρ 0 и р0 плотность и давление газа в состояние равновесия. Действительная плотность в точке Х в момент времени t – ρ(x,t).
Относительное изменение плотности
Тогда


Разность между действительным давлением Р и равновесным давлением Р0 обозначим Р'(x,t). Именно этот избыток давления производит движение микрофонной диафрагмы.
Р'(x, t) – звуковое давление
P=P0 + P’(x, t)
Сила, действующая на элемент с одной стороны, возникающая в результате давления слоёв газа


Разность между этими силами
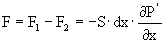
является полной силой, действующей на элемент газа, лежащей между плоскостями.
Масса газа
 ,
,
Ускорение



 - уравнение движения.
- уравнение движения.
При равновесии масса газа должна быть равна плотности  , умноженной на объём
, умноженной на объём  . Когда плоскости смещаются под действием звуковой волны, масса газа должна оставаться постоянной, т.е.
. Когда плоскости смещаются под действием звуковой волны, масса газа должна оставаться постоянной, т.е.

Когда плоскости смещены, объём может измениться, т.к. смещение одной плоскости 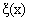 , а другой
, а другой

Объём в результате смещения

Плотность газа должна изменяться так, что общая масса


Используя введённое обозначение δ и пренебрегая величинами второго порядка малости, считая S=const
 - уравнение неразрывности.
- уравнение неразрывности.
Если плоскости в результате смещения раздвигаются, то плотность газа в данной точке уменьшается и наоборот.
III. Уравнение состояния.
Используются термодинамические свойства газов. Сжатие и расширение в звуковой волне происходят достаточно быстро, поэтому температура газа меняется при неизменной тепловой энергии –адиабатический процесс.
Он описывается следующим уравнением
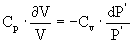
Сp , Cv- теплоёмкости при P=const и V=const. 
Подставляя значение объёма элемента газа, полученное раннее

или  ;
;  - для воздуха
- для воздуха
или с учётом закона неразрывности  - уравнение состояния.
- уравнение состояния.
Волновое уравнение.
Комбинируя уравнение I, II, III, получим



Для скорости звука в идеальном газе

Для воздуха при температуре Т=00С

Атмосферное давление
Р0=10.23 Па (10.13- 10.16)
В общем случае Р0 и ρ0 есть функции температуры.
Тогда
 , где t – температура, град С.
, где t – температура, град С.
Для воздуха С≈331.3+1.21∙t, м с.


Потенциал колебательной скорости.
Можно показать [1,стр.153-162], что колебательная скорость, в общем случае
представляющая собой векторное поле, имеет потенциальный характер (rotξ=0).
Интеграл вида 
называют потенциалом скорости.
Все функции, описывающие звуковое поле ρ, P, ξ, T ρвязаны с потенциалом скорости соотношениями


βs – адиабатическая сжимаемость


α ч –коэффициент объёмного расширения
x k=x, y, z
Используя функцию потенциала вместо трёх (шести) уравнений можно записать одно
 -
-
-волновое уравнение для потенциала скорости.
Дата добавления: 2015-09-05; просмотров: 162 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Лекция N2 | | | Элементы теории излучения |