Лекция № 1.

Основные понятия акустики. Механические колебания системы. Литература.

Акустика — наука о звуке, трактуется как механика упругих волн.

Существование упругих волн вытекает из законов Ньютона.

1. Удар по концу длинного стержня — начальное возмущение.
2. Слой, прилегающий к торцу, сжимается. Возникшие силы упругости ускоряют следующий слой и деформируют его.
3. Упругие силы, возникшие при деформации второго слоя, остановит первый слой, а второй приобретает скорость.
4. Первый слой остановился и вернулся в недеформированное состояние, и второй начал двигаться и сжался.

Движение и деформация передаются от слоя к слою, — по стержню побежит упругая волна.

Во всех случаях распространения упругих волн в любых средах — твердых, жидких, газообразных — основные черты одинаковы: частицы среды в волне приобретают скорость, деформируются и в них возникают упругие напряжения, которые передают волну дальше по телу.

При распространении волны различают два совершенно разных явления:

1. движение частиц среды в волне, как материальных точек. Характеризуется смещением и скоростью частицы. Зависят от силы звука. Эти величины, как правило, малы, а после прохождения волны каждая частица практически остается в своем исходном положении.
2. перемещение самой упругой волны по среде — характеризуется скоростью звука, которая зависит от свойств среды (упругость, плотность, вязкость и др.).

Существует два подхода к изучению упругих волн:

1. волна как движение материальных точек (частиц среды), упруго взаимодействующих между собой. Способ громоздок, т.к. частицы влияют друг на друга и необходимо анализировать поведение каждой частицы.
2. волна как самостоятельный объект. Удается найти простые законы поведения: распространение, отражение, преломление, рассеяние и т.д.

Ньютоновская механика для частиц среды используется для получения общих законов поведения упругих волн.

Хотя звуковая волна — механическое явление, поведение волны — иное, чем движение материальных тел.

Волны характеризуют непрерывным распределением в среде:

• давление
• скорости частиц
• плотности
• температуры.

Совокупность этих величин называют волновым звуковым полем.

Распространение волны — изменение волнового поля с течением время.

Среду рассматривают как сплошную.

Частица среды — любой мысленно выделенный участок среды, малый по сравнению с расстоянием, на котором свойства среды изменяются существенным образом.

Акустическое или

Звуковое давление — превышение р давления в волне над давлением р₀ в невозмущенной среде

р = р₀ + р^'.

Типы задач акустики.

1. Задачи о свободных волнах.

Нахождение волн, которые могут распространяться в неограниченной среде в отсутствие внешних воздействий.

1. Задачи с начальными условиями.

В них задается распределение давления, и скорости частиц во всей среде для некоторого начального момента времени и требуется найти волну в дальнейшие моменты времени.

1. Краевые задачи.

Изучают волны в ограниченном участке среды, свойства границ которого считают заданными.

1. Задачи о сторонних воздействиях — источниках звука.

Рассматривают звуковые волны, образованные посторонними телами, помещенными в неограниченную среду и совершающими колебания. Звуковое поле — волны, расходящиеся от колеблющихся тел в бесконечность.

1. Задачи о рассеянии от препятствий.

Отражение, прохождение звука, дифракционные задачи.

1. Задачи о затухании звука.

Большинство задач акустики сводится к комбинации типов.

Предмет цели и задачи курса.

Механические колебательные системы.

Метод электромеханических аналогий.

Акустическое поле представляет собой поле механических возмущений, поэтому для его возбуждения либо приема необходима прежде всего механическая колебательная система.

Под механической колебательной системой понимают систему, состоящую из связанных между собой твердых тел. В качестве твердых тел могут быть элементы системы, обладающие:

1. массой и не имеющие упругих свойств
2. упругостью без массы
3. одновременно упругостью и массой

Кроме того в механической системе могут быть элементы характеризующие необратимые потери при колебаниях.

Если изменения сил, смещений, скоростей, деформаций в механической системе происходят по периодическому закону, то процессы в данной системе называются колебательными. Обычно колебательные процессы происходят по гармоническому закону.

Колебания системы могут быть свободными, затухающими, вынужденными, апериодическими.

Свободными или собственными называют колебания системы по окончании некоторого переходного процесса, вызванного изменением энергии системы, при условии, что в системе есть элемент, способный запасать энергию (масса или упругость).

Если переходный процесс не имеет колебательного характера, то он является апериодическим. Свободных гармонических колебаний в такой системе не будет,т.к. она будет поглощена в элементах, вызывающих необратимые потери.

Затухающие колебания – при наличии в системе элемента трения.

Вынужденные колебания – под действием внешних гармонических сил. Могут быть в любой механической системе.

Элементарная механическая колебательная система,простейший механический осциллятор, состоит из элемента массы, упругости и трения.

1. Элемент массы (масса) – материальная точка, в которой сосредоточена конечная масса m.

(1.1)

1. Элемент упругости (упругость) – элемент механической цепи, в котором при закреплении каждой(?) из точек этого элемента при приложении к другой точке силы F относительно перемещению точек тела противодействует только упругая сила(?).Уравнение движения:

(2.1)

s – упругость, н/м

x - смещение.

1. Элемент трения - устройство, в котором любому относительному перемещению его концов противодействует только сила трения.Уравнение движения:

(3.1)

Модель осциллятора:

Невесомая пружина S закреплена одним концом, нагружена массой m. Имеется трение, которое вызывает затухание колебаний.

1.Свободные колебания.

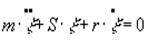(4.1)

Решение уравнения

(5.1)

A – амплитуда

- коэффициент затухания

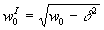; ; - гибкость

Уравнение (5.1) описывает непериодический процесс, однако при , можно говорить о квазипериодическом процессе.

Важный параметр – добротность

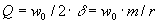
Показывает число периодов, по истечении которых амплитуда колебаний уменьшится в раз.

2.Вынужденные колебания.

(домножим обе части на 1/m) получим:

(6.1)

Общее решение - å двух функций.

(6.2)

- полное механическое сопротивление или механический импеданс осциллятора.

;

;

Выражение (6.2) описывает переходный процесс

на осциллятор на резонансной частоте воздействует гармоническая сила.

Амплитуда колебаний нарастает по закону (). В определенный момент времени работа вынуждающей силы будет компенсировать потери энергии и амплитуда колебаний будет максимальна.

- время установления колебания.

;

С момента прекращения действия силы колебания затухают по закону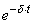

Рассмотрим установившиеся колебания.

Из (6.2) амплитуда колебания максимальна 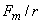при

Условие резонанса системы

;

Мощность колебаний осциллятора

; ; ;

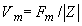На резонансе

Полоса пропускания системы º ширина резонансной кривой

- мера избирательности колебательной системы.

Q ­ - кривая уже.

[1] § 33

[4] Гл.1 § 1,2

Дата добавления: 2015-09-05