Элементы теории излучения

Задача об излучении упругих волн сводится к решению волнового уравнения относительно потенциала скорости

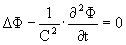
Решения волнового уравнения должны удовлетворять граничному условию на поверхности колеблющегося тела

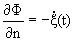
n-вектор нормали

и условию излучения

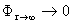
Анализируя волновое уравнение с учётом условий можно сделать следующие выводы:

1. на низких частотах, т.е. когда волновые размеры колеблющегося тела меньше 1

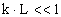
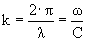-волновое число

L-линейный размер тела

или L<<λ

2) на высоких частотах,т.е. когда

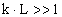
или L>>λ

Полная мощность излучения

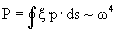-первый случай

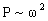-второй случай

Т.о. излучение на низких частотах малоэффективно.

Характеристики излучателей.

1. Сила реакции акустического поля.

Определим работу,которую совершает источник упругих волн против сил реакции внешней упругой среды.

Пусть элемент поверхности dS имеет нормальную составляющую колебательной скорости 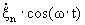и испытывает давление со стороны акустического поля

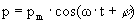
направленное на в сторону, противоположную нормали поверхности в точке dS.

Работа, совершаемая при движении всей поверхностью, против сил акустического поля за время dt (мощность в единицу времени)

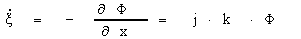
Проведя преобразования (введя в рассмотрение безразмерный вектор 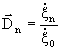, где ξ₀ –колебательная скорость точки приведения результирующих сил давления).

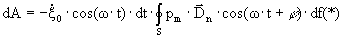
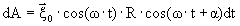
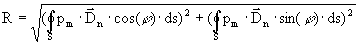
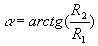
Величина 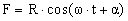имеет размерность силы и представляет интегральную силу реакции поля на поверхность излучателя или в комплексных величинах

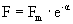
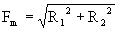
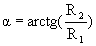
2. Механический импеданс излучателя

Механический импеданс излучателя – отношение силы реакции поля излучения, действующей на поверхность излучателя, к амплитуде колебательной скорости точки приведения ξ₀.

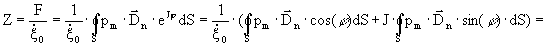
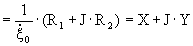
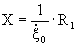-действительная часть механического импеданса

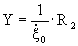-мнимая часть механического импеданса

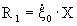
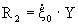
Тогда выражение для работы dA(*) преобразуется к виду

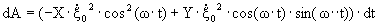
Или для мощности

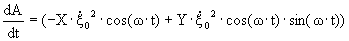
I II

Она состоит из мощности, образованной за счёт косинусной части реакции поля (или действительной части механического импеданса)-I к синусной (мнимой)-II

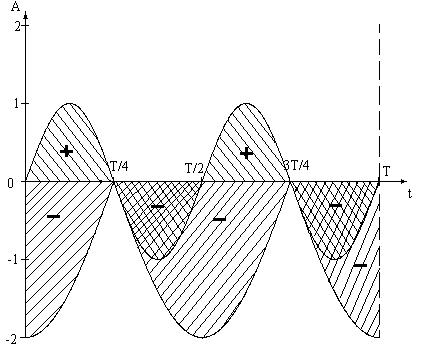
1-мощность, соответствующая косинусной составляющей силы реакции

2-мощность, соответствующая синусной составляющей.

Мощность положительна – наполнение источника излучения; мощность отрицательна – излучатель сообщает среде некоторую энергию.

Средняя мощность источника за период

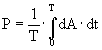
- определяется действительной частью механического импеданса.

Эта мощность непрерывно расходуется, образуя полный поток мощности акустических волн.

3. Присоединённая масса

Знакопеременная составляющая соответствует работе излучателя против синусной составляющей силы реакции поля и выражается формулами вида

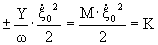
Перемена знака указывает, что через каждые четверть периода происходит попеременное накопление кинетической энергии присоединённой массы среды и возвращение этой энергии снова источнику движения поверхности излучателя.

Используя это понятие механический импеданс можно записать в виде

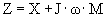
4. Предельный коэффициент эффективности акустического излучателя – отношение работы преобразователя за время Т/4, возникающей за счёт действия косинусной составляющей реакции поля к полной работе преобразователя, за то же время

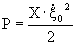- полная работа.

Работа косинусной составляющей за Т/4

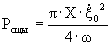
Работа синусной составляющей за Т/4

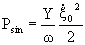
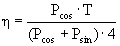
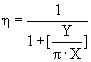
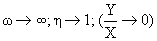
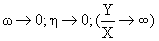
5. Характеристики направленности излучателя

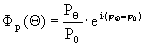
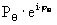- звуковое давление в точке на расстоянии R с номерным углом Θ

-на оси

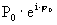1. Коэффициент осевой концентрации

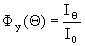
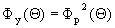
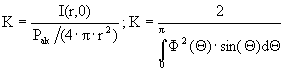
Отношение интенсивности направления излучателя 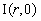, мощностью Р_ак, расположенного в точке r на оси к интенсивности ненаправленного, когда их мощности одинаковы.

Гармонические волны (плоские).

Полученному волновому уравнению удовлетворяют гармонические функции вида

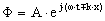
''-'' - для волн, распространяющихся в положительном направлении оси Х

''+'' – отрицательном.

Тогда для функций волнового поля получим

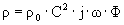
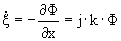
- волновое число

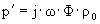
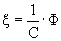
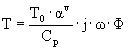
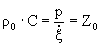-волновое или акустическое сопротивление.

Энергия плоской волны.

Кинетическая энергия элемента объёма газа

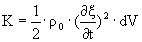
Потенциальная энергия элемента есть работа, совершаемая силами давления при сжатии элемента газа от равновесного объёма dV до некоторого нового

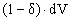
Для средних значений энергии

Средняя энергия

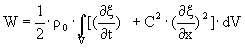
Для гармонической волны частоты f можно записать

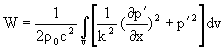
Интенсивность звука.

Количество звуковой энергии, проходящее в единицу времени через единицу площади фронта волны или поток энергии называется силой или интенсивностью звука.

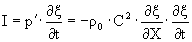
Для гармонических волн

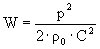
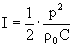
Дата добавления: 2015-09-05