Преобразование картографических проекций с использованием аппроксимирующих функций

Данный способ целесообразно использовать в случаях, когда неизвестна проекция исходного картографического мате­риала, ее формулы для определения геодезических координат (по прямоугольным) имеют сложный вид или когда картогра­фируемые территории сравнительно малы по площади.

Достоинствами этого способа являются универсальность и сравнительная простота. В нем устанавливается непосредствен­ная зависимость прямоугольных координат двух проекций и по­этому не возникает необходимости промежуточного преобразо­вания прямоугольных координат проекции исходного матери­ала в геодезические.

Однако при использовании аппроксимирующих зависимостей для преобразования систем координат в целях картографиро­вания крупных областей возникают ограничения, вызванные, главным образом, различиями в характере искажений карто­графических проекций, в характере изображения на картах географических полюсов и симметричности картографических сеток.

Эти различия требуют применения таких аппроксимирую­щих зависимостей, которые учитывали бы особенности обеих проекций. В качестве аппроксимирующих зависимостей исполь­зуются различного вида полиномы: гармонические, степенные

алгебраические, тригонометрические, мультиквадратичные, по­линомы Ньютона и др.

В случае когда карта должна быть составлена в равноуголь­ной (заданной) проекции, то независимо от проекции исход­ного картографического материала необходимо использовать либо гармонические полиномы, либо полиномы Ньютона.

В большинстве случаев более предпочтительными являются гармонические полиномы.

Формулы этих полиномов имеют вид:

где дс_и, г/_и; X, У — прямоугольные координаты проекций исход­ной и создаваемой карт; ц₀ — масштабный множитель, устанав­ливаемый из расчета, чтобы максимальные величины проме­жуточных значений £, ц были меньше единицы или равны ей; щ — постоянные коэффициенты, определяемые по способу наи­меньших квадратов; /с+1—число членов, удерживаемых в по­линомах, при этом (£+1) ^— ^п (^п — число опорных точек).

Запишем выражение (32) в матричной форме:

(34)

где

(35)

Тогда искомые постоянные коэффициенты

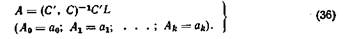
Точность определения этих коэффициентов зависит от мно­гих факторов: количества используемых опорных точек, их взаимного расположения, количества членов, удерживаемых в формулах (32) или (34), (35), (36).

В случаях когда для создания карты используются неравно­угольные проекции, то чаще всего применяют степенные алгеб­раические полиномы

где приняты обозначения (33) и ац, bij — постоянные коэффи­циенты, определяемые по способу наименьших квадратов по формулам, аналогичным (34), (35), (36). Полиномы (32), (37) даны в общем виде.

При создании карт на крупные регионы им придают конк­ретный вид с учетом условий изображения на картах геогра­фических полюсов и симметричности картографических сеток, подробно рассмотренных в работе [5].

Использование полиномов вида (32), (37) или их конкрет­ных вариантов обеспечивает возможность выполнения общих преобразований проекций, но при условии наличия аналитиче­ских комплексов с соответствующими внешними устройствами.

Однако в настоящее время преобразование проекций чаще всего приходится осуществлять на основе применения другой техники (фототрансформаторов, проекторов и т. п.) и, следо­вательно, общее преобразование заменять частными преобра­зованиями, которые соответствуют используемому типу преоб­разующих приборов.

К таким частным преобразованиям относятся*

1. Преобразования подобия (масштабные преобразования):

Х = сх; Y=cy,

где с — коэффициент изменения масштаба, для определения которого достаточно иметь две общие точки. Масштабные пре­образования выполняются с помощью редукторов, проекторов, фототрансформаторов, пантографов, фотокамер.

2. Аффинные преобразования:

X = a₀ + aix-\-a₂y,

Y=b₀ + bix+b₂y,

где а_г-, b{ — постоянные коэффициенты, для определения кото­рых достаточно иметь три общие точки, не лежащие на одной прямой. При выполнении этих преобразований прямая линия

остается прямой, частные масштабы вдоль них сохраняют по­стоянные значения, параллельные прямые остаются параллель­ными; точка, лежащая на некоторой прямой, преобразуется в точку изображения этой прямой. Аффинные преобразования осуществляются с помощью фототрансформаторов, перспекто-графов.

3. Томографические (коллинеарные) преобразования

где a_h b_u ci — постоянные коэффициенты, для определения ко­торых необходимо иметь четыре пары соответственных точек, не коллинеарных по три.

Аналогично предыдущему преобразованию здесь прямые преобразуются в прямые. Каждая точка прямой также изобра­жается точкой на изображении этой прямой, но частые мас­штабы вдоль соответственных линий будут переменными вели­чинами.

Для выполнения томографических преобразований могут быть использованы фототрансформаторы и перспектографы.

4. Преобразования второго порядка и выше (как и преды­
дущие) успешнее всего выполнять с помощью ЭВМ и состыко­
ванными с ними устройствами ввода и вывода изображений.

Но для этих целей могут быть использованы фототрансфор­маторы (ФТБ) со щелевой приставкой, дифференциальные и электронные фототрансформаторы.

Дата добавления: 2015-10-13