Преобразование картографических проекций с использованием строгих аналитических зависимостей

При выполнении картосоставительских работ, особенно при создании мелкомасштабных карт, нередки случаи, когда кар­тографические проекции исходного материала и создаваемой карты различаются между собой и возникает задача преобра­зования первой проекции (изображения) во вторую.

Общие уравнения исходной картографической проекции:

x = h(B, L), y=h(B, L). (6)

Общие уравнения проекции создаваемой карты:

X=F_l{B, L), Y = F₂(B, L), (7)

здесь fi, J2, F\, F₂ — функции однозначные, конечные, дважды дифференцируемые и независимые; х, у; X, У; В, L — соответст­венно прямоугольные и геодезические координаты точек проек­ции и поверхности эллипсоида. Из уравнения (6) запишем

B = h(x, у), L = f_A(x, у). (8)

Подставив (8) в выражение (7), найдем

Х = МЫ*. У), М*. y)] = *i{x, у);

(9) У = F* 1/з (х, у), П (*. у)] = Ф₂ (х, у).

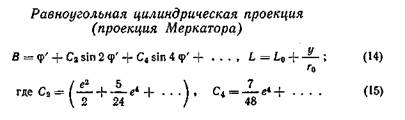
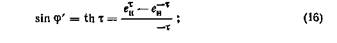
Из этих уравнений следует, что существуют два основных спо­соба преобразования изображений (картографических проек­ций). Первый способ предполагает предварительное определе­ние геодезических координат по прямоугольным. Он имеет ряд преимуществ по сравнению со вторым способом, выражаемым уравнениями (9), так как свободен от всяких ограничений.

В данном параграфе рассмотрим преобразование картогра­фических проекций эллипсоида с использованием строгих аналитических зависимостей. Этот способ позволяет осущест­вить общее преобразование в пределах всей карты и особенно целесообразен при картографировании крупных по площади областей.

Так как вычисление прямоугольных координат проекций осуществляется по известным зависимостям (7), то для пре­образования картографических проекций достаточно только определить геодезические координаты точек поверхности эллип­соида по прямоугольным координатам этих точек в проекции исходного материала (6). Ниже приведены формулы определе­ния геодезических координат для картографических проекций, которые нашли наиболее широкое применение при создании карт.

Равноугольная проекция Гаусса — Крюгера

(применительно к эллипсоиду Красовского и с погрешностью не более 0.1")

х, у — прямоугольные координаты проекции Гаусса — Крюгера, L₀ — долгота среднего (осевого) меридиана, п — целая часть числа, а — дробная часть числа.

Координаты, определяемые по формулам (10), получаются в радианах.

Промежуточные значения q/ и т вычисляются по формулам

<£ + ^ен

т=—; (17)

Го

где х, у — прямоугольные координаты проекции Меркатора, г₀ — радиус кривизны параллели с широтой Во, е — первый эксцент­риситет эллипсоида, е_н — основание натуральных логарифмов.

Равноугольные конические проекции

х=—\п( — ^с Л, (18)

^a Ч1/(_Рю-х)² + (/² /

L^L₀ + — arctg/— ^y—), (19)

а \ р_ю — х I

где а, с — постоянные параметры конической проекции; х, у — прямоугольные координаты точек в равноугольной конической проекции; р_ю — полярное расстояние южной параллели.

Записав с учетом (18) выражение (16), вычисляем искомые широты по формулам (14) и (15), а долготы — по формуле (19).

Равноугольные азимутальные (стереографические) проекции

Проекции, используемые для изображения полярныхобластей

_т=1п------ ^rjY± ------, (20)

(*2 ₊2,2)1/2

L = L₀ + arctg JL. (21)

Здесь обозначено:

(22)

Величины г_к, V_K и simJ)_K вычисляются для параллели с широ­той В_к, на которой принято, что частные масштабы длин равны единице;^*, у — прямоугольные координаты в данной стереогра­фической проекции; к — номер параллели.

Используя значения т из формулы (20) и записав выраже­ние вида (16), вычисляем искомые широты по формулам (14), (15) и долготы по формуле (21).

Проекции, получаемые как частные случаи проекции Лагранжа

где k, p —постоянные параметры проекции Лагранжа (а=1). Вычислив по формуле (23) значения т, находим sinq/ из (16), затем определяем искомые широты точек по формулам (14), (15) и долготы по (24).

Равнопромежуточные вдоль меридианов (вертикалов) «двойные» азимутальные проекции

— для эллипсоида Красовского;

/ а п =

а + 6

По полученным значениям z и а_сф вычисляем промежуточные значения

S

где Bq, L_Q — геодезические координаты точки полюса проекции (как правило, средней точки картографируемой территории).

Долготы точек будут равны L = X, L₀ = X₀-

Используя значения ф'" = т, вычисляем искомые широты В точек поверхности эллипсоида по формулам (для эллипсоида Красовского)

44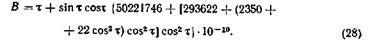

Картографические проекции международной карты мира масштаба 1:2 500 000

Для создания этой карты применяются две равнопромежу­точные вдоль меридианов проекции: конические, имеющие два постоянных параметра а и с; азимутальные, которые могут рассматриваться как частный случай конических проекций при а=1.

(29) (30)

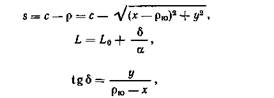(31)

где а, с — постоянные параметры проекций; р_ю — полярное расстояние южной параллели; р, б — плоские полярные коор­динаты.

Искомые широты В определяются (для эллипсоида Красов­ского) по формулам (28) и (12), в которых вместо х исполь­зуются значения s; долготы определяются по формулам (31) и (30).

Дата добавления: 2015-10-13