Труды ЦНИИГАиК. Вып. 97, 1953; вып. 132, 1960.

воспользоваться графическим способом преобразования геоде­зической системы координат исходного картматериала в геоде­зическую систему координат создаваемой карты. Для этого на прозрачный пластик в масштабе создаваемой карты наносят координатную сетку, углы рамок трапеции и тригонометриче­ские пункты в принятой для создания карты системе геодези­ческих координат, изображение которых имеется на исходном картографическом материале.

Этот пластик накладывают на исходный картматериал или на голубые копии с него, изготовленные на пластике или на бумаге, наклеенной на жесткую основу. Совместив идентичные пункты пластика и исходного материала, устанавливают, име­ются ли смещения координатных сеток и углов рамок трапе­ций на пластике относительно их изображения на картмате-риале. Отсутствие таких смещений свидетельствует о том, что исходный картматериал и создаваемая карта имеют единую систему координат. Если такие смещения имеются, то с пла­стика перекалывают на исходный картматериал (голубые ко­пии) углы рамок трапеции и координатную сетку, что и обес­печивает желаемое преобразование геодезических систем коор­динат.

Более строго эта задача решается аналитически — путем введения так называемых дифференциальных поправок первого и второго рода. Во многих книгах по высшей и сфероидической геодезии даны формулы для определения дифференциальных поправок первого рода {dB\", dL_x"), учитывающих изменения начала координат и азимута в начальном (исходном) пункте, и второго рода (dB₂", dLJ'), учитывающих изменения сжатия и большой полуоси исходного и нового эллипсоидов. В приве­денных формулах ряд членов представлен в функции азимутов, изменений длины геодезической линии и т. п., что неудобно при решении задач картографии. Ниже даны несколько преобра­зованные формулы, ошибки определения поправок по которым не будут превосходить 10 м или 0,3".

с координатами B_u L\ дифференциальные поправки первого рода, т. е. поправки за изменение начала координат и азимута; da, da — изменения сжатия и большой полуоси эллипсоида; dB₀", dL₀", dHo" — известные в нулевой точке (B₀,L₀) диффе­ренциальные поправки второго рода, т. е. поправки за размеры эллипсоида и его ориентировку.

Значение / определяется из уравнений проекций:

I" вычисляют 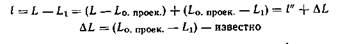приближенно с использованием формул проек­ций (см. § 10).

Например, для проекции Гаусса — Крюгера будем иметь

sin/"» (1 -\ e'²sin²v J г,

где е' — второй эксцентриситет эллипсоида;

z= ^y; a cos v

cos / = cos /" cos M — sin I" sin AL; sin / = sin I" cos &L + cos I" sin M. v принимает следующие значения:

X

•v = t = — p'—для проекции Гаусса — Крюгера;

•v = т = ——-------- для проекции Гаусса — Боага (V ТМ);

Я-0,9996 ^F

«v = t = — р'—для трапециевидной псевдоцилиндрической про-

R екции, равновеликой псевдоконической проекции Бонна, про­стой поликонической проекции, для «двойных» проекций: стереографических, равнопромежуточных азимутальных, попе­речно-цилиндрических проекций (s — длина дуги мериди­ана, р' — радиан в минутах); v = arcsin[tht)—для проекции Меркатора, равноугольной конической проекции, азимутальной равноугольной проекции (в нормальной ориентировке), для про­екции Лагранжа и т. д.

Дата добавления: 2015-10-13