Основные положения расчета на прочность роторов центрифуг

Нагрузка, действующая на ротор. Основной деталью большинства конструкций роторов центрифуг является цилиндрическая или коническая обечайка (рис. 3.21б). Напряжения в обечайке ротора возникают под действием: а) центробежных сил инерции собственных масс конструкции; б) гидравлического давления центрифугируемой жидкости, вращающейся вместе с ротором.

а

б

в

Рисунок 3.21 -Схема ротора

a – структура сил во вращающемся цилиндре; б – основные конструктивные параметры; в – форма свободной поверхности жидкости во вращающемся цилиндре с крышкой

Нагрузка от собственных сил инерции ротора.

Пусть – интенсивность сил инерции массы обечайки – сила инерции массы обечайки, приходящаяся на единицу ее боковой поверхности.

Она равна

(3.78)

Нагрузка от сил инерции жидкости. Найдем теперь удельное давление вращающейся жидкости на обечайку ротора.

Рассмотрим прямой круговой цилиндр, закрытый снизу днищем, а сверху – кольцевой крышкой и вращающийся с угловой скоростью w вокруг своей вертикальной оси. Ввиду симметрии системы ограничимся рассмотрением осевого сечения цилиндра с системой координат x, y (рис. 3.21а).

Предполагаем, что жидкость вращается вместе с цилиндром, не перемещаясь относительно его стенок. На элементарную массу dm на свободной поверхности вращающейся жидкости действует центробежная сила и сила тяжести , результирующая которых должна быть перпендикулярна поверхности, являющейся поверхностью уровня. Если касательная к сечению поверхности, то

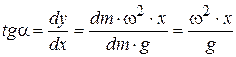, (3.79)

Интегрируя, находим уравнение сечения свободной поверхности поверхностью xy

, (3.80)

Полученное выражение - уравнение параболы, отнесенной к осевой оси. Следовательно, свободная поверхность жидкости - параболоид вращения.

При , имеем 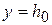, следовательно и

, (3.81)

При 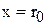имеем и 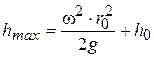, (3.82)

Из уравнения (3.82), приняв, находим, что скорость, при которой жидкость поднимается на высоту h

, (3.83)

При скорости вращения 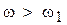жидкость будет стремиться подняться на высоту 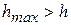и при отсутствии крышки начнет переливаться через край. Так как крышка этого не допускает, жидкость начнет скапливаться под крышкой и покроет ее по кольцу с внутренним радиусом r (рис. 3.21в).

Рассуждая совершенно так же, как в случае открытого цилиндра, мы приходим к выводу, что уравнение (3.80) остается в том же виде, другим будет лишь значение постоянной С, которое мы найдем, приняв в уравнение (3.80) при

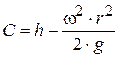, , (3.84)

Подставляя значение С в уравнение (3.80), получим

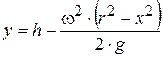
, (3.85)

Из уравнения (3.85) имеем 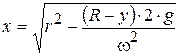, (3.86)

При получаем 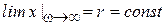, (3.87)

т.е. при достаточно больших скоростях вращения ротора (соответствующих рабочим условиям) свободная поверхность жидкости может считаться цилиндрической.

Установив форму свободной поверхности во вращающемся цилиндре, найдем теперь давление ее на обечайку.

Давление жидкости на обечайку. Выделим в кольце вращающейся жидкости элементарное кольцо массой ,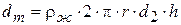

Центробежная сила, действующая на это кольцо, равна .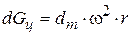

Давление от этой силы на соседний слой жидкости

, (3.88)

Давление на обечайку ротора

, (3.89)

, (3.90)

где r, r ₀ – внутренний и наружный радиусы слоя жидкости в роторе.

Умножив и разделив правую часть на , получаем

, (3.91)

где 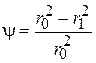– степень заполнения ротора; V – окружная скорость ротора, м/с.

Расчет цилиндрической обечайки ротора по безмоментной теории. Согласно мембранной (безмоментной) теории тангенсальное напряжение в обечайке, нагруженной внутренним давлением, равно

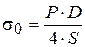
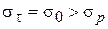; , (3.92)

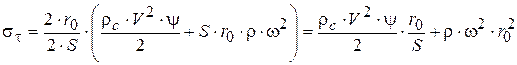, (3.93)

, (3.94)

где 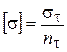– допускаемое напряжение для материала ротора, МПа/м²;
j – коэффициент ослабления сварного шва.

Учет перфораций в роторе. Перфорированные элементы роторов центрифуг рассчитываются на прочность как сплошные эквивалентные элементы, имеющие такие же приведенные физические характеристики: плотность r, модуль упругости Е, коэффициент ослабления сварного шва j.

Данная методика расчета применима для роторов, изготовленных из пластичных материалов, при условии, что выполняются неравенства

, (3.95)

где r_отв – радиус отверстия, м; F_отв – площадь всех отверстий перфорированного элемента, м²; F – площадь срединной поверхности сплошного элемента, м²; r ₀ – радиус срединной поверхности ротора.

Формулы для пересчета величин Е, r, j имеют вид

, (3.96)

, (3.97)

, (3.98)

где поправочный коэффициент С_n рассчитывается по формуле

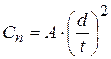, (3.99)

Здесь А – коэффициент, зависящий от схемы разбивки отверстий;
d – диаметр отверстий, м; t – шаг между отверстиями, м.

Коэффициент ослабления j _n применяется в расчете вместо коэффициента jсварного шва формула (3.94) в том случае, когда , в противном случае j _n вообще не применяется.

Дата добавления: 2015-10-13