
Читайте также:
|
77. Дано натуральне число п. Обчислити:
а) 
б) n!
в) 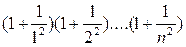 ;
;
г)  ;
;
д)  ;
;
e) 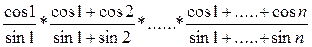 ;
;
78. Дано дійсне число а, натуральне число л. Обчислити;
а)  ;
;
б) а(а + 1)...(а + n -1);
в)  ;
;
г)  ;
;
д) а (а - n)(а - 2n)...(а - n2).
79. Обчислити (l+sin0.1)(l-sin 0.2)……(l + sin 10).
80. Дано дійсне число n:. Обчислити

81. Дано дійсні числа х, а, натуральне число п обчислити
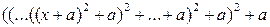
82. Дано дійсне число х. Обчислити:

83. Дано дійсне число а. Знайти:
а) серед чисел  …..перше більше а;
…..перше більше а;
б) таке найменше п, що  >a
>a
84. Дано натуральне n, дійсне х. Обчислити:
а) sin х + sin2 х +... + sinn х;
б) 
 в) sin x + sin sin x +... + sin sin...sin x.
в) sin x + sin sin x +... + sin sin...sin x.
|
85. Дано дійсні числа a, h, натуральне число п.
Обчислити
f(a)+2f(a+h)+2f{a+2h)+......+2f(a+(n—1)h)+f(a+nh),
де
f(x)=(x2+ l)cos2x.
86. Дано натуральне число п.
а) Скільки цифр у числі, n?
б) Чому дорівнює сума його цифр?
в) Знайти першу цифру числа п.
г) Знайти знакочергуючу суму цифр числа n (нехай запис п у десятковій системі є 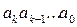 ; знайти.
; знайти. 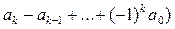
87. Дані натуральні числа п, т. Одержати суму m останніх, цифр числа п.
88. Дано натуральне число п.
а) З'ясувати, чи входить цифра 3 у запис числа п2.
б) Поміняти порядок цифр числа п на зворотний.
в) Переставити першу й останню цифри числа п.
г) Приписати по одиниці в початок і в кінець запису числа п
89. Алгоритм Евкліда перебування найбільшого загального дільника (НОД) ненегативних цілих чисел заснований на наступних властивостях цієї величини. Нехай т і п - одночасно не рівні нулю цілі ненегативні числа і нехай т>п. Тоді, якщо n = 0, то (НОД) (п, т)=т, а якщо п=0, то для чисел т, п і r, де r –залишок від розподілу т на п, виконується рівність НОД (m, п} =НОД(n, r). Наприклад, НОД(15, 6)=НОД(6, 3)= = НОД(3, 0)=3.
Дано натуральні числа п, т.
а) Використовуючи алгоритм Евкліда, знайти найбільший загальний дільник п і т.
б) Знайти найменше загальне кратне п і т, (Як тут може допомогти алгоритм Евкліда?)
90. Дано натуральні числа т і п. Знайти такі натуральні р і q, що не мають загальних дільників, що p/q = m/n.
91. Нехай

Дано натуральне число п. Отримати 
92. Нехай

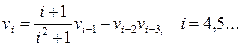
Дано натуральне п (n > 4). Одержати 
93. Нехай

Дано дійсні q, r, b, c, d, натуральне п (п >2).
Одержати 
94. Нехай
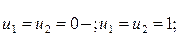

 i=3,4..
i=3,4..
95. Нехай
a0=a1=1; ai=ai-2+ai-1/2i-1; i=2,3,…..
Знайти добуток а0*а1*а2.....а14
96. Нехай
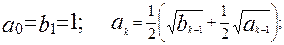

98. Нехай

99. Нехай

Данні дійсні u,v натуральні n. Знайти
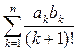
100. Нехай
 i=4,5,…
i=4,5,…
Знайти

101 Дані позитивні дійсні числа а, х, е. У послідовності  , утвореної за законом
, утвореної за законом
 i=1,2……,
i=1,2……,
знайти перший, член  для якого виконана нерівність
для якого виконана нерівність

102. Нехай
 k=1,2…..
k=1,2…..
Знайти перший член  , для якого
, для якого  .
.
103. Нехай
 k=1,2..
k=1,2..
Дано дійсне a > 0. Знайти перший член  , для якого виконано
, для якого виконано 
104. Дано дійсне a >0. Послідовність  ... утворена за законом
... утворена за законом
Знайти перший член  , для якого
, для якого 
Обчислити для знайденого значення  різниця
різниця 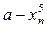 .
.
105. Дано натуральне число л, дійсне число х.
Обчислити:
а) 
б)  .
. 
106. Дано дійсні числа а, b, натуральне число п (b > а). Одержати (f1 +... + fn) h, де
 i=1,2,…,n.
i=1,2,…,n.
107. Дано ціле число m > 1. Одержати найбільше ціле k, при якому  .
.
108.. Дане натуральне число п. Одержати найменше ціле виду  , що перевершує п.
, що перевершує п.
109. Дано натуральне число п. Обчислити
1*2+2*3*4+…+n*(n+1)*…*2n
110. Обчислити


111. Дано дійсне число x = О. Обчислити

……………….

112. Дано цілі числа n, k (n>k>0). Обчислити

113./'Нехай п - дійсне число і нехай n!! означає 1 3 5…… п для непарного п і 2 4..... п для парного п.
Для заданого натуральних я обчислити:
а) a!!;
b) 
114. Обчислити:
a) 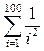 ; б)
; б) 
в)  г)
г) 
д)  е)
е) 
ж) 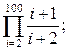 з)
з) 
115. Дано натуральне число п. Обчислити:
а)  б)
б) 
в)  г)
г) 
д)  е)
е) 
ж) 
116. Дано натуральне число п, дійсне число х
Обчислити:
а)  б)
б) 
в)  г)
г) 
д) 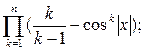 е)
е) 
117. Дано натуральне число п. Обчислити добуток перших п співмножників:
а) 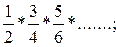
б) 
118 Обчислити  слідуючими чотирма способами:
слідуючими чотирма способами:
а) послідовно зліва направо;
б) послідовно зліва направо обчислюються  і
і 
потім друге значення віднімається з першого;
в) послідовно праворуч ліворуч;
г) послідовно праворуч ліворуч обчислюються суми, написані в б), потім-віднімання.
Чому при обчисленнях на обчислювальній машині кожним з цих способів виходять різні результати?
119. Обчислити нескінченну суму з заданою точністю e (е > 0). Вважати, що необхідна точність досягнута, якщо обчислена сума декількох перших доданків і черговий доданок виявився по модулі менше, ніж е, - ці і всі наступні доданки можна вже не враховувати. обчислити:
а)  б)
б) 
в)  г)
г) 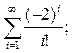
д)  е)
е) 
Дата добавления: 2015-10-13; просмотров: 97 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Найпростіша цілочислена арифметика | | | Найпростіші графічні побудови |