Розгалуження

33. Дані дійсні числа х, у,. Одержати

а) max(x,y);

б) min (x, y);

в) max(x,y), min (x,y).

34. Дані дійсні числа х, у, z. Одержати:

a) max(x,y,z);

б) min(x, у, z), тах (х, у, z).

35. Дано дійсні числа х, у, z. Обчислити:

а) тaх (х+у+z, хуz);

б) min²(x+y+z/2, хуz)+ 1.

36. Дано дійсні числа а, b, с. Перевірити, чи виконуються нерівності а < b < с.

37. Дано дійсні числа а, b, с. Подвоїти ці числа, якщо а>b>c, і замінити їхніми абсолютними значеннями, якщо це не так.

38. Дано дійсні числа x, у. Обчислити z;

39. Дано два дійсних числа. Вивести перше число, якщо воно більше другого, і обидва числа, якщо це не так.

40. Дано два дійсних числа. Замінити перше число нулем, якщо воно менше чи дорівнює другому, і залишити числа без зміни в противному випадку,

41. Дано три дійсних числа. Вибрати з них ті, котрі належать інтервалу (1, 3).

42. Дано дійсні числа х, у (х=у). Менше з цих двох чисел замінити їхньою напівсумою, а більше— їхнім подвоєним добутком.

43. Дано три дійсні числа. Звести в квадрат ті з них, значення яких ненегативні.

44. Якщо сума трьох попарно різних дійсних чисел х, у, z менше одиниці, то найменше з цих трьох чисел замінити напівсумою двох інших; у противному випадку замінити менше з х i у напівсумою двох значень, що залишилися.

45. Дано дійсні числа а, b, c, d. Якщо a<b<c<d, то кожне число замінити найбільшим з них; якщо а>b>c>d, то числа залишити без зміни; у противному випадку всі числа заміняються їхніми квадратами.

46. Дано дійсні числа х, у. Якщо х і у від’ємні, то кожне значення замінити його модулем;

якщо негативне тільки одне з них, то обидва значення збільшити на 0.5; якщо обидва значення ненегативні і жодне з них не належить відрізку [0.5, 2.0], тоді обидва значення зменшити в 10 разів; в інших випадках х и у залишити без зміни.

47. Дано дійсні позитивні числа х, у, z

а) З'ясувати, чи існує трикутник з довжинами сторін х, y, z.

б) Якщо трикутник існує, тo чи є він гострокутним.

48. Дано дійсні числа a, b, c (а=0). З'ясувати, чи має рівняння дійсні корені. Якщо дійсні корені є, то знайти їх. У противному випадку відповіддю повинне служити повідомлення, що дійсних коренів немає.

49. Дано дійсне число А. З'ясувати, чи має рівняння дійсні корені, якщо

;

;

.

Якщо дійсні корені існують, то знайти їх. У противному випадку відповіддю повинне служити повідомлення, що дійсних коренів нема.

50. Дано дійсні числа a1,b1,c1,a2,b2,c2.З'ясувати, чи вірно, що(a1b2-a2b1)>0.0001 і якщо вірно, те знайти рішення системи лінійних рівнянь

a1x+b1y+c1=0

a2x+b2y+c2=0

(при виконанні виписаної нерівності система свідомо разом і має єдине рішення).

51. Дано дійсні числа а, b, с, (а=0). Цілком досліджувати біквадратне рівняння , тобто якщо дійсних коренів немає, те повинне бути видане повідомлення про це, інакше повинні бути видані два чи чотири корені.

52. Дано дійсні числа а, Ь, с, d, s, t, и (s і t одночасно не дорівнюють нулю). Відомо, що точки (а, b ) і (с, d} не лежать на прямої l заданої рівнянням, sx+ty+u=0. Пряма l розбиває координатну площини на двох напівплощин. З'ясувати, чи вірно, що точки (а, b) і (с, d) належать різним напівплощинам.

53. Дано дійсні числа а, b с, d, e, f, g, h. Відомо, що точки (е, f) і (g, h) різні. Відомо:

також, що точки (а, b ) і (с, d) не лежать прямій l, що проходить через, точки (c, f) і (g, h). Пряма l розбиває координатну площину на двох напівплощин. З'ясувати, чи вірно, що точки (а, b) і (c, d) належать однієї і тієї ж напівплощини.

54. Дано дійсні числа . Чи належить початок координат трикутнику з вершинами

55. Дано дійсні позитивні числа а, b, c, d. З'ясувати, чи можна прямокутник зі сторонами а, b умістити усередині прямокутника зі сторонами c, d так, щоб кожна зі сторін одного прямокутника була паралельна або перпендикулярна кожный стороны прямокутника.

56. Дано дійсні позитивні числа a, b, c, х, у. З'ясувати, чи пройде цегла з ребрами а, b, c у прямокутний отвір зі сторонами х i у. Просовувати цегла в отвір дозволяється тільки так, щоб кожне з його ребер було рівнобіжно чи перпендикулярно кожної зі сторін отвору.

57. Дано дійсне число a. Обчислити f (a), якщо

a)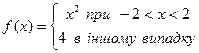

б)

в)

г)

58. Дано дійсне число а. "Для функцій f(x), графіки яких представлені на мал. 1, а—1, г, обчислити f(a}.

 

 

 

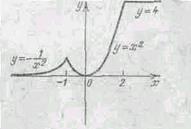
59. Дано дійсні числа х, у. Визначити, чи належить крапка з координатами х, у заштрихованої частини площини (мал.. 2, а- 2, к).

60. Нехай D-заштрихована частина площини (мал. 3, а—3, е) і нехай і визначається по х і у наступним

образом (запис (х, y) Є D. означає, що крапкам координатами х, у належить D):

а)

б)

в)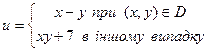

г)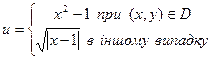

д)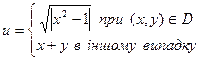

е)

Дана дійсні числа х, у. Визначити u.

Дата добавления: 2015-10-13