Анализ цепи

Представим исходную цепь в виде Г-образного соединения

Рисунок 11– Исходная цепь

Тогда передаточная функция:

;

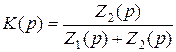где ;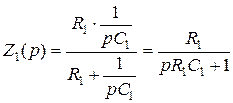

.

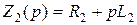Подставим Z₁(p) и Z₂(p) и преобразуем:

.

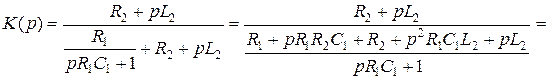
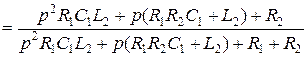Переходную характеристику g(t) найдем следующим образом

.

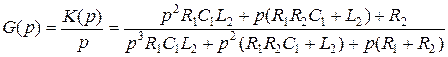Подставим исходные данные и разложим знаменатель на множители:

.

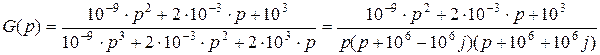То есть G(p) имеет три полюса:

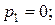
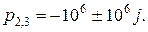
Найдем вычеты относительно этих полюсов:

;

;

.

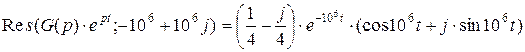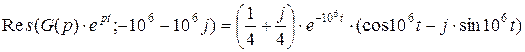Тогда выражение для оригинала переходной характеристики можно найти как сумму вычетов, помноженную на функцию включения:

.

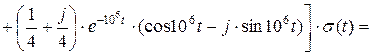
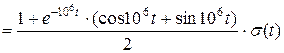График переходной характеристики цепи представлен на рисунке 2.2:

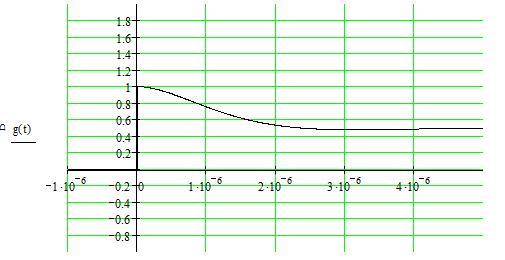
Рисунок 11 – Переходная характеристика цепи

Импульсная характеристика h(t) может быть найдена по известному выражению для переходной характеристики следующим образом:

.

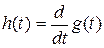На основе вышеуказанной формулы:

.

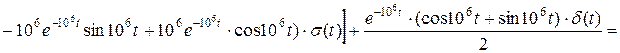
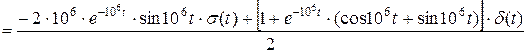График импульсной характеристики цепи представлен на рисунке 2.3:

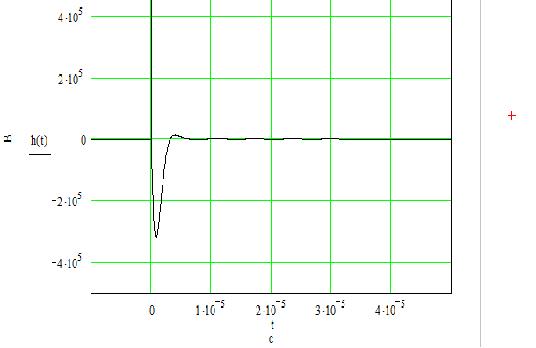
Рисунок 12– Импульсная характеристика цепи

Комплексный коэффициент передачи цепи находится из выражения для передаточной функции переходом :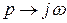

.

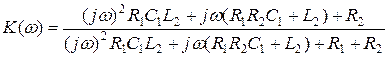Подставляя исходные значения и преобразуя, получим:

.

Амплитудно-частотная характеристика цепи находится взятием модуля от комплексного коэффициента передачи:

.

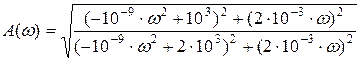График АЧХ цепи представлен на рисунке13:

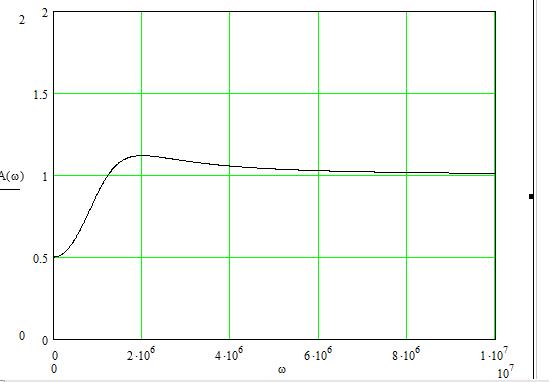
Рисунок 13 – Амплитудно-частотная характеристика цепи

Фазо-частотная характеристика цепи есть аргумент от комплексного коэффициента передачи:

.

График ФЧХ цепи представлен на рисунке 14:

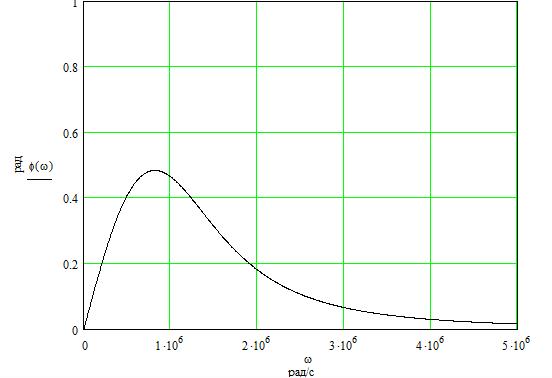
Рисунок 14– Фазо-частотная характериистика цепи

Дата добавления: 2015-09-03