Собственный вектор

Собственным вектором линейного преобразования называется такой ненулевой вектор, что для некоторого

15. Собственное число

Собственным значением линейного преобразования называется такое число, для которого существует собственный вектор.

16. Характеристический многочлен (формула)

характеристическим многочленом квадратной матрицы называется многочлен

17.

1)

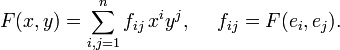
2)

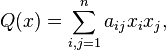
18.

А=Ат - симметрическая матрица.

А=-Ат - антисимметрическая матрица.

19.

Ортогональное дополнение подпространства векторного пространства с билинейной формой — это множество всех векторов, ортогональных каждому вектору из подпространства.

20.

Квадратичную форму f(x) называют положительно (отрицательно) определенной, если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е. f(X) > 0 (отрицательна, т.е.
f(X) < 0).

21.

Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.

Пусть квадратичная форма имеет в каком-то базисе матрицу

Критерий положительной определённости квадратичной формы.

Для положительной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры её матрицы были положительны.

Критерий отрицательной определённости квадратичной формы.

Для отрицательной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры чётного порядка её матрицы были положительны, а нечётного порядка — отрицательны.

22.

оператор называется нильпотентным, если некоторая его степень есть нулевой оператор.

23.

Жорданова матрица — квадратная блочно-диагональная матрица над полем , с блоками вида

24.

Составим бесконечный матричный степенной ряд

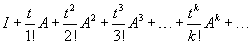
Сумма данного бесконечного ряда называется матричной экспонентой и обозначается как exp (tA):

Дата добавления: 2015-09-03