
Читайте также:
|
Прежде чем переходить к решению второго из поставленных в § 6.2 вопросов, рассмотрим важный частный случай, когда множества решений и u значений параметров l непрерывны и имеют одинаковую структуру.
Как отмечалось выше, в этом случае решение и может быть интерпретировано как оценка параметра l, а правило решения u = u(x) ставит в соответствие каждому значению х значение этой оценки. Будем считать, что функция потерь является симметричной функцией разности
u - l, тогда апостериорный риск
 (6.3.1)
(6.3.1)
Пусть плотность совместного распределения вероятности  дважды дифференцируема по
дважды дифференцируема по  и
и  при любых значениях
при любых значениях  ,
,  , тогда
, тогда
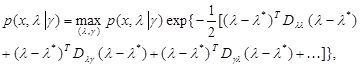 (6.3.2)
(6.3.2)
где  ,
,  - решение уравнения
- решение уравнения
 (6.3.3)
(6.3.3)
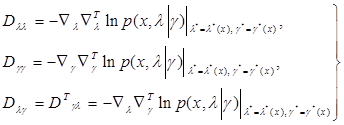 (6.3.4)
(6.3.4)
взятые со знаком минус матрицы, составленные из вторых производных логарифма плотности  в точке
в точке  ,
,  , которые подобно
, которые подобно 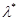 и
и  зависят только от х;
зависят только от х;  - оператор градиента по компонентам
- оператор градиента по компонентам  ;
; 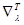 ,
, 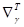 - операторы градиента, ставящие в соответствие той функции, на которую действуют такие операторы, вектор-строку частных производных этой функции по всем компонентам
- операторы градиента, ставящие в соответствие той функции, на которую действуют такие операторы, вектор-строку частных производных этой функции по всем компонентам  или
или  . Не написанные в показателе экспоненты (6.3.2) члены имеют третий и более высокий порядок относительно разностей
. Не написанные в показателе экспоненты (6.3.2) члены имеют третий и более высокий порядок относительно разностей  и
и  . Роль этих членов тем меньше, чем больше объем данных наблюдения х; по мере его увеличения совместное распределение вероятности
. Роль этих членов тем меньше, чем больше объем данных наблюдения х; по мере его увеличения совместное распределение вероятности  при заданном х и величины
при заданном х и величины  из (6.3.3) асимптотически приближаются к нормальному распределению вероятности. Используя это асимптотическое приближение, получаем
из (6.3.3) асимптотически приближаются к нормальному распределению вероятности. Используя это асимптотическое приближение, получаем
 , (6.3.5)
, (6.3.5)
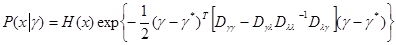 , (6.3.6)
, (6.3.6)
где  - как всегда матрица, обратная матрице
- как всегда матрица, обратная матрице  ;
;  - некоторая неотрицательная функция, зависящая только от х.
- некоторая неотрицательная функция, зависящая только от х.
Из выражения для апостериорного риска (6.3.5) следует, что оптимальная байесова оценка 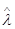 параметра
параметра  имеет вид
имеет вид
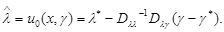 (6.3.7)
(6.3.7)
Действительно, благодаря свойствам функции потерь g(u - l) выражение (6.3.6) дифференцируемо по u под знаком интеграла, при этом  - нечетная функция своего аргумента и, следовательно, при подстановке u = u0(x,
- нечетная функция своего аргумента и, следовательно, при подстановке u = u0(x,  ) из (6.3.7) градиент
) из (6.3.7) градиент  обращается в нуль, то есть обеспечивается минимум апостериорного риска.
обращается в нуль, то есть обеспечивается минимум апостериорного риска.
Из выражения (6.3.6) следует, что оценка максимального правдоподобия параметра  , определяемая как решение уравнения (6.2.15), совпадает с величиной
, определяемая как решение уравнения (6.2.15), совпадает с величиной  *, являющейся решением уравнения (6.3.3). Поэтому адаптивное байесово правило решения принимает вид
*, являющейся решением уравнения (6.3.3). Поэтому адаптивное байесово правило решения принимает вид
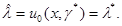 (6.3.8)
(6.3.8)
Тем самым уравнение (6.3.3) дает полное решение задачи - оно определяет наилучшее в условиях априорной неопределенности решение задачи оценивания l и дает оценку максимального правдоподобия для параметра  , описывающего неопределенность априорных знаний о законах распределения вероятности х и l.
, описывающего неопределенность априорных знаний о законах распределения вероятности х и l.
Покажем, что правило решения (6.3.8) удовлетворяет требованию (6.2.12) равномерно наилучшего приближения к оптимальному байесову решению с известным значением  . Ограничимся для простоты случаем квадратичной функции потерь
. Ограничимся для простоты случаем квадратичной функции потерь

Вычисляя значения апостериорного риска (6.3.5) при  , где
, где 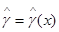 - какая либо оценка
- какая либо оценка  , и при
, и при  и беря их разность, получаем следующее выражение для функции
и беря их разность, получаем следующее выражение для функции
 (6.3.9)
(6.3.9)
где 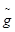 - симметричная квадратная матрица того же порядка, что и вектор
- симметричная квадратная матрица того же порядка, что и вектор  , не зависящая от
, не зависящая от  и
и  , но, возможно, зависящая от х.
, но, возможно, зависящая от х.
Величина разности средних рисков адаптивного и оптимального при известном  байесовых правил решения
байесовых правил решения  будет при этом равна
будет при этом равна
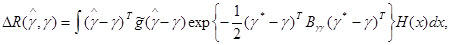 (6.3.10)
(6.3.10)
где для сокращения записи обозначено
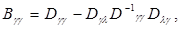 (6.3.11)
(6.3.11)
Математическое ожидание матрицы 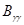 представляет собой информационную матрицу Фишера для совокупности параметров g.
представляет собой информационную матрицу Фишера для совокупности параметров g.
Из выражения (6.3.10) видно, что задача нахождения минимаксной оценки  , обеспечивающей выполнение требования (6.2.12), в данном случае с точностью до обозначений совпадает с рассмотренной в § 5.2. Из полученного там решения следует, что минимаксная оценка параметра g есть g*(x) и, следовательно, правило решения (6.3.8) действительно обеспечивает равномерно наилучшее приближение к минимальному байесову среднему риску для известного значения g.
, обеспечивающей выполнение требования (6.2.12), в данном случае с точностью до обозначений совпадает с рассмотренной в § 5.2. Из полученного там решения следует, что минимаксная оценка параметра g есть g*(x) и, следовательно, правило решения (6.3.8) действительно обеспечивает равномерно наилучшее приближение к минимальному байесову среднему риску для известного значения g.
Дата добавления: 2015-09-03; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| АДАПТИВНЫЙ БАЙЕСОВ ПОДХОД ПРИ ПАРАМЕТРИЧЕСКОЙ АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТИ | | | Принцип минимакса |