Ограниченные сведения о множестве допустимых значений

Аналогичные предыдущим результаты получаются в том случае, когда априорная информация относительно l, ограничена знанием толь­ко множества L допустимых значений l. При этом наименее предпочти­тельное распределение, естественно, обращается в нуль для lÎL, а ми­нимаксное решение в довольно широких условиях совпадает с оценкой максимального правдоподобия, вычисленной при нахождении максиму­ма функции правдоподобия по ограниченному множеству значений lÎL. Рассмотрим для примера достаточно важный и широко распространен­ный на практике случай, о котором шла речь в § 3.1, когда допустимое множество значений l={l₁,...... l_n} ограничено совокупностью гиперпо­верхностей в n-мерном пространстве, задаваемых с помощью соотноше­ния

, (5.3.1)

где f() - некоторая векторная функция f()={f₁(),..., f_n()} вектор­ного параметра ={ ₁,., _n}, (m<n), который может принимать лю­бые значения в m-мерном евклидовом пространстве.

В этом случае функция правдоподобия для интересующих нас зна­чений lÎL, где множество L задается с помощью (5.3.1),

(5.3.2)

является фактически функцией только параметра а. Подобно этому функция потерь

(5.3.3)

тоже является функцией параметра a. Поэтому, если для параметра a существует такая достаточная статистика z = z(x), что аналогично (5.2.2)

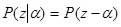(5.3.4)

и для решения u(x) = f(z(x)) функция потерь (5.3.3) может быть представлена в виде

(5.3.5)

где g₂(z - а) - симметричная функция разности z - а, то совершенно аналогично § 5.2 доказывается, что правило решения

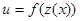(5.3.6)

является минимаксным правилом - минимаксной оценкой вектора l (соответственно достаточная статистика z(x) является минимаксной оценкой векторного параметра ). Наименее предпочтительное распре­деление l в данном случае - равномерное распределение на множест­ве L, заданном соотношением (5.3.1).

Достаточная статистика z(x), как следует из (5.3.4), является также оценкой максимального правдоподобия и может быть найдена, из соотношения

(5.3.7)

в котором максимизация по производится для всех возможных зна­чений , принадлежащих m-мерному евклидову пространству.

Важным частным случаем рассматриваемой задачи является слу­чай, когда множество L - совокупность некоторых гиперплоскостей n-мерного пространства l.. При этом функции f(a) линейные, то есть

(5.3.8)

где F = ||F_ik|| - некоторая матрица порядка (n x m), а оптимальная минимаксная оценка l, имеет вид

(5.3.9)

где *(х) - оценка максимального правдоподобия параметра .

Представление (5.3.5).для функции потерь в этом случае автома­тически имеет место, если g(u,l) - произвольная симметричная функ­ция разности u - l.

Ход рассуждений при получении решений (5.3.6), (5.3.9) совсем не требовал, чтобы пространство значений l было конечномерным. Очевидно, полученные результаты справедливы и тогда, когда это пространство имеет более сложную структуру. Например, пусть нас интересует задача оценки функции l(t) на интервале (t₁, t₂), причем этот интервал может быть и бесконечным. В этом случае множество значений l- функциональное пространство. В свою очередь, функция l (t) может быть векторной, то есть l(t) = {l⁽¹⁾(t),…, l^(l)(t)}, где l - чис­ло компонент этой векторной функции. Ограничения на множество возможных значений l, (5.3,1) при этом принимают вид

(5.3.10)

где f - скалярная либо векторная (f = {f⁽¹⁾,…, f ^(l))}, функция времени и параметра ={ ₁,...... _n}, а решение - оценка функции l(t):

(5.3.11)

где * = *(x) = z(x) - оценка максимального правдоподобия для параметра , получаемая из соотношения

(5.3.12)

Таким образом, решение (5.3.11) дает оптимальный минимаксный алго­ритм фильтрации (построения оценки функций времени) для широкого класса задач, в которых искомые в процессе фильтрации функции могут быть описаны с помощью зависимости (5.3.10), содержащей произ­вольное число полностью неизвестных параметров { ₁,...... _m}. Примеры подобного описания на практике весьма многочисленны: траектория движения объекта, для которого дифференциальные уравнения движе­ния известны, а начальные условия неизвестны; процессы, соответству­ющие уравнениям движения, которые содержат какие-либо неизвест­ные параметры или коэффициенты, и т. д.

Дата добавления: 2015-09-03