Вводные замечания. Из результатов предыдущей главы видно, что нахождение оценок максимального

Из результатов предыдущей главы видно, что нахождение оценок максимального правдоподобия является существенным элементом адап­тивного байесова подхода и до некоторой степени даже его основой в случае параметрически заданной априорной неопределенности. Метод максимального правдоподобия, как мы видели ранее в гл. 2, 4, 5, имеет и большое самостоятельное значение. Он позволяет в ряде случаев най­ти минимаксное решение задачи с гарантированным уровнем риска и дает возможность выявить достаточные или квазидостаточные статисти­ки. В связи с этим в настоящей главе более подробно рассмотрим мето­ды получения и свойства оценок максимального правдоподобия.

Этому вопросу посвящена довольно обширная литература, начиная сранних работ по классической математической статистике, поэтому, возможно, значительная часть того, что будет изложено ниже, хорошо известна многим читателям. Это в особенности относится к случаю ре­гулярных оценок по совокупности независимых данных наблюде­ния, соответствующему этому случаю неравенству Крамера-Рао и асимптотической эффективности регулярных оценок максимального правдоподобия. Наряду с этим имеется много сравнительно малоиз­вестных аспектов метода максимального правдоподобия: влияние ста­тистической зависимости данных наблюдения на сходимость и точность оценок максимального правдоподобия; нерегулярность, когда функция правдоподобия недифференцируема по оцениваемым параметрам; ре­куррентные процедуры нахождения оценок максимального правдоподо­бия и их свойства и т. д. Наличие подобных аспектов, а также большое значение метода максимального правдоподобия для решения задач син­теза в условиях априорной неопределенности делают целесообразным систематическое изложение основных фактов, относящихся к методам получения и свойствам оценок максимального правдоподобия. Большин­ство этих фактов будет приведено без доказательства со ссылками на оригинальные и популярные работы, в которых такие доказательства имеются.

Прежде чем перейти к дальнейшему изложению, напомним некото­рые основные определения. Пусть имеется совокупность данных наблю­дения 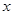, которую обычно будем представлять в виде вектора , каждая компонента которого соответствует одному наблюде­нию и, в свою очередь, может быть вектором того или иного порядка или даже отрезком реализации некоторого непрерывного случайного процесса. Пусть эти данные наблюдения зависят от некоторого парамет­ра размерности . 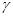(Нам удобно ввести здесь новое обозначение для неизвестных параметров, чтобы иметь возможность в дальнейшем понимать под как параметры , характеризующие ап­риорную неопределенность в статистическом описани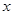и и 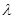, так и сами параметры 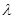, влияющие на последствия принимаемых решений и являющиеся предметом оценки в исходной задаче статистического ре­шения, так и, наконец, совокупность тех и других параметров.) Зависи­мость данных наблюдения 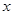от параметров описывается функцией правдоподобия

(7.1.1)

где - плотность совместного распределения вероятности при заданном значении , а оценка максимального прав­доподобия 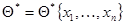определяется из уравнения максимального правдоподобия

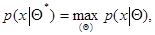(7.1.2)

где максимум находится по области допустимых значений . Уравнение (7.1.2) эквивалентно следующему уравнению для логарифма функции правдоподобия, которым часто будем пользоваться в дальнейшем:

(7.1.3)

где

(7.1.4)

Если для каждого из допустимого множества значений для почти всех значений 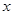существуют частные производные 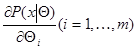причем

где - интегрируемые по всему пространству 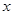функции, то оценка максимального правдоподобия является регулярной и уравнение макси­мального правдоподобия может быть представлено в одной из эквива­лентных форм

(7.1.5)

или

(7.1.6)

где - оператор градиента по компонентам век­тора .

Регулярный случай, пожалуй, чаще всего встречается на практике. Однако во многих важных практических задачах свойство регулярности не выполняется, что заставляет рассматривать и более общий случай, для которого некоторые закономерности поведения регулярных оценок могут и не соблюдаться. Если наряду с оценкой максимального правдоподобия 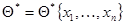рассмотреть какую-либо другую функцию , которая не является решением уравнения максимального прав­доподобия, то очевидно, что при весьма общих предположениях о виде этой функции можно считать ее оценкой параметра , более того, и совершенно произвольную функцию вектора можно также назвать оценкой , хотя возможно, что точность этой оценки будет со­вершенно неудовлетворительной. В дальнейшем нам понадобится опре­деление регулярности и для оценки произвольного вида. Чтобы ввести это определение, зададим взаимно однозначное преобразование

(7.1.7)

где - некоторая многомерная функция дополняющая преобразование до взаимно однозначного. В силу взаимной однозначности этого преобразования две совокупности и статистически эквивалентны, по­этому вместо исходной совокупности данных наблюдения можно рассматривать преобразованную совокупность статистическое описание которой задается функцией правдоподобия , получающейся применением преобразования (7.1.7) к исходной функции правдоподобия (7.1.1).

Функцию правдоподобия , очевидно, можно записать в виде

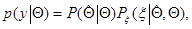(7.1.8)

где и - соответствующие условные плотности ве­роятности. Оценка называется регулярной, если для каждого из заданного множества значений для почти всех значений и существуют частные производные , причем

где и - функции, интегрируемые по всему пространству и 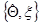соответственно.

Совокупность этих условий несколько жестче, чем простое требова­ние дифференцируемости функции правдоподобия. Они накладывают определенные ограничения не только на , но и на возможные виды преобразования , то есть на структуру оценочных функций.

Всякая оценка отличается от истинного значения . Про­стейшей характеристикой этого отличия является математическое ожи­дание разности

(7.1.9)

вообще говоря, зависящее от и называемое смещением оценки. Оцен­ка, для которой называется несмещенной.

Важным понятием является также понятие достаточной оценки. Оценка называется достаточной, если условная плотность ве­роятности в (7.1.8) не зависит от . Достаточная оценка является, очевидно, минимальной достаточной статистикой для пара­метра : достаточной в силу того, что она удовлетворяет основному требованию к любой достаточной статистике (гл. 2), а минимальной - в силу того, что размерность этой статистики (вектора ) совпадает с размерностью вектора неизвестных параметров . Если существует какая-либо достаточная оценка , то любая лучшая оценка может быть только функцией .

Дата добавления: 2015-09-03