
|
Читайте также: |
Несколько последующих глав будет посвящено детальному рассмотрению адаптивного байесова подхода при наличии параметрической априорной неопределенности применительно к широким классам задач с доведением правил решения до детальной структуры и исследованием эффективности этих правил решения. В этой главе на ряде примеров, каждый из которых также относится к достаточно широкой совокупности задач, проиллюстрируем возможности адаптивного байесова подхода в непараметрическом случае.
В § 6.1 мы уже рассмотрели пример применения адаптивного байесова подхода в случае непараметрической априорной неопределенности (пример 2). Этот пример в некотором отношении является крайним: характер априорной неопределенности таков, что какие-либо сведения об аналитическом описании исходного материала полностью отсутствуют: совсем неизвестно распределение вероятности наблюдаемых значений  (
( ),полностью неизвестен вид функции потерь и тем более природа и статистическое описание параметров
),полностью неизвестен вид функции потерь и тем более природа и статистическое описание параметров 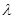 , влияющих на величину потерь и последствия от принятия того или иного решения.
, влияющих на величину потерь и последствия от принятия того или иного решения.
Нужно отметить, что за эту крайность приходится расплачиваться довольно серьезными ограничениями: предположениями о дискретности множества решений U, о дискретности множества значений  , о независимости и одинаковости распределений вероятности всех значений
, о независимости и одинаковости распределений вероятности всех значений  (
( ), об одинаковости истинных (неизвестных нам) функций потерь на всех шагах
), об одинаковости истинных (неизвестных нам) функций потерь на всех шагах  и требованием, чтобы полная совокупность данных наблюдения х содержала значения принятых при
и требованием, чтобы полная совокупность данных наблюдения х содержала значения принятых при 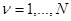 N решений
N решений  и появившихся при этом потерь
и появившихся при этом потерь  . Указанные ограничения выражают иную форму представления имеющихся априорных знаний, отличную от параметрического статистического описания неизвестных распределений вероятности и функций потерь, причем, как видно из перечисленных ограничений, необходимый для нахождения правила решения объем этих априорных знаний довольно велик.
. Указанные ограничения выражают иную форму представления имеющихся априорных знаний, отличную от параметрического статистического описания неизвестных распределений вероятности и функций потерь, причем, как видно из перечисленных ограничений, необходимый для нахождения правила решения объем этих априорных знаний довольно велик.
Возникающее иногда противопоставление параметрического и непараметрического подходов к решению задач синтеза и обсуждение, какой из них является более подходящим в условиях априорной неопределенности и соответствует более глубокой степени этой неопределенности, представляются довольно беспочвенными: параметрическое и непараметрическое описания исходных данных задачи просто соответствуют разным видам имеющихся ограниченных априорных знаний и взаимно дополняют друг друга.
Характерной чертой непараметрического случая является использование в той или иной степени эмпирических распределений вероятности вместо истинных и эмпирических средних значений вместо математических ожиданий, подобно тому, как это было сделано в примере 2 § 6.1 при замене апостериорного риска (условного математического ожидания функции потерь) его оценкой - эмпирическим средним значением ожидаемых при данном результате наблюдения потерь. Это обстоятельство приводит к определенным требованиям к объему и составу полной совокупности данных наблюдения х, для того чтобы эмпирическое осреднение приводило к состоятельным оценкам необходимых для отыскания правил решения математических ожиданий (среднего риска, апостериорного риска, минимального значения апостериорного риска и т. д.). Указанная совокупность х должна иметь вполне определенный состав и содержать достаточное для построения таких оценок количество данных наблюдения.
Так, в условиях примера 2 § 6.1 (при неизвестной функции потерь) совершенно необходимо, помимо величин  (
(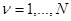 ), знать значение принятого при каждом
), знать значение принятого при каждом 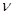 решения
решения  и величину потерь
и величину потерь  от принятия этого решения. В противном случае никакого адаптивного байесова или любого другого правила решения, обладающего хотя бы свойством асимптотической оптимальности, построить невозможно.
от принятия этого решения. В противном случае никакого адаптивного байесова или любого другого правила решения, обладающего хотя бы свойством асимптотической оптимальности, построить невозможно.
В этом отношении непараметрические задачи имеют широкий спектр возможностей: чем больше объем наших сведений (качественного или количественного характера) об аналитических свойствах распределений вероятности х и 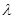 , и функций потерь, тем менее жесткие требования предъявляются к составу и объему совокупности данных наблюдения и наоборот.
, и функций потерь, тем менее жесткие требования предъявляются к составу и объему совокупности данных наблюдения и наоборот.
8.4. НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ СОГЛАСИЯ
В гл. 4 мы уже упоминалиоб обширном классе двухальтернативных задач, связанных с проверкой гипотезы о том, что совокупность наблюдаемых данных подчиняется некоторому заданному распределению вероятности при свободной альтернативе, то есть в предположении, что наряду с выполнением этой гипотезы могут встретиться какие угодно случаи. Там же был рассмотрен пример такой задачи в параметрическом варианте, когда класс возможных распределений вероятности ограничен некоторым параметрическим семейством с совершенно произвольными значениями параметров. При отсутствии такого ограничения задача приобретает дополнительную специфику, связанную с очень большой степенью априорной неопределенности и необходимостью ей непараметрического решения. Правило решения этой задачи, по установившейся терминологии, называется критерием согласия и неоднократно рассматривалось в литературе по математической статистике, являясь классическим примером задачи принятия решения в условиях априорной неопределенности. Покажем, как получить известные и новые непараметрические критерии согласия на основе адаптивного байесова подхода.
Сформулируем более четко постановку задачи. Пусть имеется совокупность независимых наблюдений  и функция распределения величины
и функция распределения величины  (
( ) есть либо
) есть либо  , либо
, либо  , причем функция распределения
, причем функция распределения 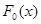 известна, а функция распределения
известна, а функция распределения  полностью неизвестна и совершенно произвольна. На основании наблюдения совокупности данных
полностью неизвестна и совершенно произвольна. На основании наблюдения совокупности данных  требуется решить, какая из альтернатив имеет место в действительности:
требуется решить, какая из альтернатив имеет место в действительности:
1)  - выборка
- выборка 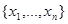 описывается распределением вероятности с функцией распределения
описывается распределением вероятности с функцией распределения 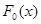 ;
;
2)  - выборка
- выборка 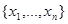 не описывается распределением вероятности с функцией распределения
не описывается распределением вероятности с функцией распределения 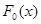 , а описывается распределением вероятности с какой-то иной отличной от
, а описывается распределением вероятности с какой-то иной отличной от 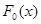 , функцией распределения
, функцией распределения  .
.
Обозначим решения, состоящие в принятии первой и второй альтернативы, через  и
и  соответственно и определим функцию потерь
соответственно и определим функцию потерь 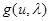 . Обычно для правильных решений принимаются нулевые потери
. Обычно для правильных решений принимаются нулевые потери  , а значение потерь от принятия решения
, а значение потерь от принятия решения  (решение о том, что выборка не согласуется с заданной функцией распределения
(решение о том, что выборка не согласуется с заданной функцией распределения 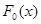 , когда на самом деле совокупность данных
, когда на самом деле совокупность данных 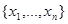 описывается функцией распределения
описывается функцией распределения 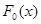 , (
, ( )) может быть принято равным произвольной константе, без ограничения общности
)) может быть принято равным произвольной константе, без ограничения общности  . Потери
. Потери  от принятия решения
от принятия решения  о том, что выборка описывается функцией распределения
о том, что выборка описывается функцией распределения 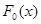 , когда на самом деле она не описывается ей (
, когда на самом деле она не описывается ей ( ), естественно задать так, чтобы они были малы, если различие между функциями распределения
), естественно задать так, чтобы они были малы, если различие между функциями распределения 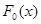 и
и  мало, и увеличивались по мере роста различий между этими функциями распределения, то есть
мало, и увеличивались по мере роста различий между этими функциями распределения, то есть  .
.
Для того чтобы задача имела нетривиальное решение, функционал 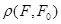 должен обращаться в нуль при
должен обращаться в нуль при  . Это естественное требование соответствует тому очевидному факту, что при
. Это естественное требование соответствует тому очевидному факту, что при  потери должны обращаться в нуль, поскольку вторая альтернатива совпадает с первой. В качестве функционала
потери должны обращаться в нуль, поскольку вторая альтернатива совпадает с первой. В качестве функционала 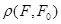 , удовлетворяющего всем перечисленным требованиям, удобно взять ту или иную меру различия в функциональном пространстве функций распределения. Примерами таких мер являются
, удовлетворяющего всем перечисленным требованиям, удобно взять ту или иную меру различия в функциональном пространстве функций распределения. Примерами таких мер являются
 , (8.4.1)
, (8.4.1)
 , (8.4.2)
, (8.4.2)
и т. д.
 . (8.4.3)
. (8.4.3)
Зададим также априорные вероятности альтернатив  ,
,  и введем произвольное рандомизированное правило решения, определив для этого решающую функцию (
и введем произвольное рандомизированное правило решения, определив для этого решающую функцию (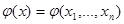 - вероятность принять решение
- вероятность принять решение  , если наблюдаемая совокупность данных есть
, если наблюдаемая совокупность данных есть  . Тогда средний риск
. Тогда средний риск
 (8.4.4)
(8.4.4)
естественно зависит от неизвестной функции распределения  и поэтому также неизвестен.
и поэтому также неизвестен.
Предположим на время, что функция распределения  известна и равна
известна и равна  , то есть речь идет о задаче проверки гипотезы с простой заданной альтернативой
, то есть речь идет о задаче проверки гипотезы с простой заданной альтернативой  . Тогда, применяя обычный байесов подход, получаем нерандомизированное правило решения:
. Тогда, применяя обычный байесов подход, получаем нерандомизированное правило решения:
 или
или  при
при  . (8.4.5)
. (8.4.5)
Неравенство (8.4.5), определяющее условия принятия решения 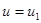 о том, что выборочные данные согласуются с распределением вероятности, задаваемым функцией распределения
о том, что выборочные данные согласуются с распределением вероятности, задаваемым функцией распределения 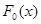 , можно переписать в следующем виде:
, можно переписать в следующем виде:
 , (8.4.6)
, (8.4.6)
где  - некоторая функция выборочных данных, определяемая при известной
- некоторая функция выборочных данных, определяемая при известной  левой частью неравенства (8.4.5).
левой частью неравенства (8.4.5).
При неизвестной функции распределения  в соответствии с общими принципами адаптивного байесова подхода нужно заменить неизвестные нам статистические описания данных наблюдения оценочными значениями, полученными с помощью тех же данных наблюдения. В данном случае нам неизвестны как функция потерь - величина
в соответствии с общими принципами адаптивного байесова подхода нужно заменить неизвестные нам статистические описания данных наблюдения оценочными значениями, полученными с помощью тех же данных наблюдения. В данном случае нам неизвестны как функция потерь - величина 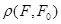 , зависящая от неизвестной функции распределения
, зависящая от неизвестной функции распределения  - так и отношение правдоподобия
- так и отношение правдоподобия  , входящее в функцию С = С (х) и зависящее от неизвестной плотности вероятности
, входящее в функцию С = С (х) и зависящее от неизвестной плотности вероятности  . Состоятельной оценкой функции распределения
. Состоятельной оценкой функции распределения  в предположении, что имеет место вторая альтернатива, является выборочная функция распределения
в предположении, что имеет место вторая альтернатива, является выборочная функция распределения
 , (8.4.7)
, (8.4.7)
где
 (8.4.8)
(8.4.8)
а состоятельной оценкой 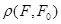 - величина
- величина
 , (8.4.9)
, (8.4.9)
которая зависит от совокупности имеющихся данных  . Нужно отметить, что, используя (8.4.7), мы уже израсходовали все имеющиеся данные наблюдения на оценку функции распределения
. Нужно отметить, что, используя (8.4.7), мы уже израсходовали все имеющиеся данные наблюдения на оценку функции распределения  и функции потерь
и функции потерь 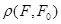 . Такая политика в отношении распределения имеющейся информации для устранения априорной неопределенности является в данном случае правильной, поскольку все равно без дополнительных предположений о возможном виде функции распределения
. Такая политика в отношении распределения имеющейся информации для устранения априорной неопределенности является в данном случае правильной, поскольку все равно без дополнительных предположений о возможном виде функции распределения  (то есть ограничения второй альтернативы) никакой состоятельной оценки плотности вероятности
(то есть ограничения второй альтернативы) никакой состоятельной оценки плотности вероятности  и функции правдоподобия, входящей в величину С = С (х), не существует. Лучшее, что можно сделать в этих условиях - заменить в (8.4.6)
и функции правдоподобия, входящей в величину С = С (х), не существует. Лучшее, что можно сделать в этих условиях - заменить в (8.4.6) 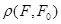 его состоятельной оценкой
его состоятельной оценкой  из (8.4.9), а
из (8.4.9), а  - некоторой константой.
- некоторой константой.
В результате приходим к следующему правилу решения, определяющему непараметрический критерий согласия: решение 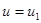 о том, что совокупность данных наблюдения
о том, что совокупность данных наблюдения  подчиняется распределению с функцией распределения
подчиняется распределению с функцией распределения 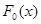 , принимается в том случае, если выполняется неравенство
, принимается в том случае, если выполняется неравенство
 (8.4.10)
(8.4.10)
Различным определениям меры различия 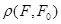 соответствуют разные критерии согласия: для (8.4.1) получается критерий Колмогорова, для (8.4.2) - критерий w2 Мизеса - Смирнова и т. д. Константа С в (8.4.10) обычно выбирается так, чтобы вероятность принять решение
соответствуют разные критерии согласия: для (8.4.1) получается критерий Колмогорова, для (8.4.2) - критерий w2 Мизеса - Смирнова и т. д. Константа С в (8.4.10) обычно выбирается так, чтобы вероятность принять решение 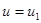 , когда выполняется первая альтернатива (
, когда выполняется первая альтернатива ( ), была равна заданной величине.
), была равна заданной величине.
Правило решения(8.4.10) обладает следующими свойствами асимптотической инвариантности: при  распределение вероятности случайной величины
распределение вероятности случайной величины  в случае, если выборка
в случае, если выборка 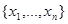 описывается функцией распределения
описывается функцией распределения 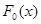 , не зависит от вида этой функции, то есть получается универсальным для всех
, не зависит от вида этой функции, то есть получается универсальным для всех 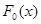 , а в случае, если выборка описывается функцией распределения
, а в случае, если выборка описывается функцией распределения 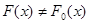 , зависит от истинной величины
, зависит от истинной величины 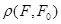 . Асимптотические свойства критериев согласия (8.4.10) и их поведение при конечных п подробно исследованы в литературе по математической статистике.
. Асимптотические свойства критериев согласия (8.4.10) и их поведение при конечных п подробно исследованы в литературе по математической статистике.
Совершенно аналогично можно получить решение некоторых более сложных задач проверки гипотезы со свободной альтернативой. Пусть, например, имеется две совокупности данных наблюдения  и
и  и требуется решить, подчиняются ли они одному и тому же распределению вероятности (на этот раз неизвестному) или нет. Если обозначить
и требуется решить, подчиняются ли они одному и тому же распределению вероятности (на этот раз неизвестному) или нет. Если обозначить
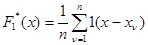 ,
,  , (8.4.11)
, (8.4.11)
выборочные фикции распределения, построенные по совокупности х и у соответственно, то аналогично (8.4.10) правило решения для этой задачи определяется следующим неравенством:
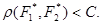 (8.4.12)
(8.4.12)
При этом меру  обычно задают так, что она удовлетворяет требованиям, вытекающим из обычного определения расстояния, то есть
обычно задают так, что она удовлетворяет требованиям, вытекающим из обычного определения расстояния, то есть 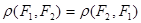 . (Заметим, что функции
. (Заметим, что функции  из (8.4.2), (8.4.3) не отвечают этому свойству.) В частности, для
из (8.4.2), (8.4.3) не отвечают этому свойству.) В частности, для 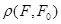 из (8.4.1) получаем известный критерий Смирнова.
из (8.4.1) получаем известный критерий Смирнова.
Можно еще усложнить постановку задачи с учетом возникающих практических потребностей. Пусть, например, задана некоторая функция  , и производятся две независимые серии наблюдений
, и производятся две независимые серии наблюдений  и
и 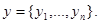
Требуется принять решение, связаны ли эти величины заданной функциональной зависимостью, то есть являются ли случайные величины 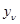 значениями функции
значениями функции  от случайного аргумента
от случайного аргумента  , с тем же распределением вероятности, что и любая из величин
, с тем же распределением вероятности, что и любая из величин  . Осуществим преобразование случайных величин
. Осуществим преобразование случайных величин  в соответствии с правилом
в соответствии с правилом  , в результате чего получим совокупность данных
, в результате чего получим совокупность данных 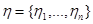 . Тогда поставленная задача статистического решения сводится к задаче проверки гипотезы о том, что совокупности
. Тогда поставленная задача статистического решения сводится к задаче проверки гипотезы о том, что совокупности  и у подчиняются одному и тому же распределению вероятности, а непараметрическое правило ее решения дается неравенством (8.4.12), где
и у подчиняются одному и тому же распределению вероятности, а непараметрическое правило ее решения дается неравенством (8.4.12), где
 . (8.4.13)
. (8.4.13)
В заключение отметим, что приведенные в этой главе примеры применения адаптивного байесова подхода, несмотря на довольно значительную общность каждого из них, ни в коей мере не исчерпывают даже небольшой доли того громадного множества задач, которое возникает в практических приложениях. Однако читатель получил определенное представление о возможностях применения адаптивного байесова подхода к задачам с непараметрической априорной неопределенностью и сможет применить при необходимости изложенные выше методы.
Дата добавления: 2015-09-03; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Рекуррентные методы | | | ОЦЕНКА ПЕРЕМЕННЫХ ПАРАМЕТРОВ |