Конечные методы

При решении уравнения правдоподобия (7.1.2), (7.1.3) может быть использован любой из известных методов максимизации функции век­торной переменной . Только в редких случаях максими­зирующее значение - оценка максимального правдоподобия нахо­дится точно. В частности, это заведомо удается сделать, если функция правдоподобия такова, что

(7.5.1)

где матрица положительно (или отрицательно) определен­ная при всех 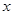и , а уравнения

(7.5.2)

имеют решения. Эти решения

(7.5.3)

где - функция, обратная , и являются компонентами вектора оцен­ки максимального правдоподобия.

Простейшим частным случаем (7.5.1) является случай, когда лога­рифм функции правдоподобия квадратично зависит от , то есть

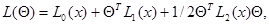(7.5.4)

где 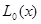- скаляр; - вектор той же размерности т, что и ; - неособая матрица порядка . При этом оценка максималь­ного правдоподобия

(7.5.5)

где - матрица, обратная .

Другим распространенным примером, для которого выполняется (7.5.1), является случай, когда

(7.5.6)

В этом случае оценка максимального правдоподобия

(7.5.7)

Число таких примеров, как соответствующих (7.5.1), так и несоот­ветствующих этому условию, но допускающих точное решение уравнения правдоподобия, в том числе и для нерегулярного случая (примеры § 7.4 и др.), довольно велико, однако еще более многочисленны случаи, когда точное аналитическое решение уравнения правдоподобия получить невозможно. При этом для нахождения оценки используются различ­ные приближенные методы. Выбор того или иного из них определяется исходя из точности приближенного решения и вычислительной просто­ты. В частности, в регулярном случае широко распространены различ­ные варианты итеративных процедур, в том числе градиентный метод, метод наискорейшего спуска, метод Ньютона, метод золотого сечения и т.д. Любой из них является методом последовательных приближений и при определенных условиях обеспечивает достаточно быструю схо­димость к истинному решению уравнения максимального правдоподо­бия. Приведем для примера алгоритм нахождения оценки максималь­ного правдоподобия, соответствующий методу Ньютона. В этом случае k-я итерация, определяющая очередное приближение к оценке мак­симального правдоподобия , производится по правилу

, (7.5.8)

где - приближение, полученное на -м шаге, а начальное приближение выбирается произвольно с учетом имеющихся представлений о существе задачи. Входящий в (7.5.8) оператор представляет со­бой результат умножения вектора-столбца на транс­понированный ему вектор (строку) и является матрицей вида так что результат воздействия этого опе­ратора на функцию также представляет собой матрицу

(7.5.9)

a , как всегда, обратная матрица.

Проиллюстрируем применение этого алгоритма на примере оценки единственного параметра 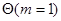для случая, когда логарифм функ­ции правдоподобия представляется в виде

(7.5.10)

где х - вектор некоторой размерности; - некоторые функ­ции х; - известная величина, функция имеет единственный мак­симум (для определенности при ) и является четной относительно этого значения, а суммирование производится по такому множеству значений j, что интервал от до 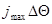полностью перекрывает диапазон возможных значений параметра . К функции правдоподобия, соответствующей (7.5.10), приводят многие задачи радиотехнических измерений (частоты, задержки радиолокационного сигнала, направле­ния на источник излучения).

Выберем в качестве нулевого приближения для оценки макси­мального правдоподобия 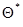величину, соответствующую какому-либо из дискретных значений , например 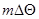. Для того чтобы это значение давало максимально возможную величину функции правдоподобия, очевидно, его нужно выбрать так, чтобы

(7.5.11)

В силу свойств функции выбор любого другого т приведет к уменьшению логарифма функции правдоподобия. Таким образом, наи­более правдоподобным дискретным приближением к оценке максималь­ного правдоподобия является величина

(7.5.12)

где m определяется условием (7.5.11) и соответствует тому номеру j, для которого величина максимальна.

Следующее приближение вычисляется в соответствии с алгорит­мом Ньютона (7.5.8) и дается выражением

(7.5.13)

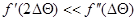где учтена четность функции . Если последняя, как это бывает в практических задачах, достаточно быстро убывает с увеличением , так что и , то в числителе и знаменате­ле выражения (7.5.13) можно ограничиться только первыми слагаемы­ми. В результате

(7.5.14)

то есть оценка получается зависящей только от наибольшей из величин и двух ближайших к ней. Приближение (7.5.14), как правило, оказывается достаточно точным, и следующие итерации не требуются.

Дата добавления: 2015-09-03