Критерій Лапласа

Критерій Лапласа використовується при умові, коли ймовірності можливих станів систем невідомі, тобто в умовах повної невизначеності. Він базується на використанні принципу недостатнього обґрунтування, який стверджує, що стани системи 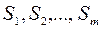мають рівні ймовірності. Враховуючи вищесказане, початкову задачу можна розглядати як задачу прийняття рішень в умовах ризику, коли вибирається альтернатива а _і, яка дає найбільш очікуваний виграш R ₁(коли 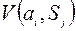моделює прибуток) або найменший очікуваний програш R ₁(коли 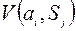моделює витрати). Отже, для знаходження величини R ₁ має місце:

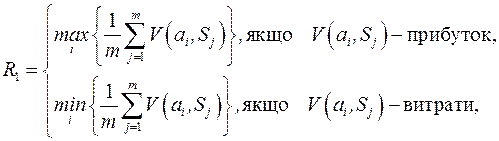(13.1)

де 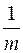– імовірність реалізації стану .

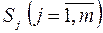Критерій Лапласа доцільно використовувати в тих випадках, коли різниця між окремими станами системи велика, тобто велика дисперсія значень.

Приклад 13.1. Підприємство повинно визначити рівень виробництва певного виду продукції так, щоби задовольнити потребу споживачів протягом певного періоду часу. Конкретна кількість споживачів невідома, але очікується, що вона може становити одне з п'яти значень: 250, 300, 350, 400, або 450. Для кожного з цих можливих значень існує найкращий рівень пропозиції чи найкраща альтернатива (з точки зору можливих затрат). Відхилення від цих рівнів приводить до додаткових витрат або через перевищення пропозиції над попитом, або через неповне задоволення попиту. Розмір втрат (тис. грн.) наведений у табл. 13.1. Використовуючи критерій Лапласа, знайти оптимальну альтернативу.

Таблиця 13.1

Альтернатива	Споживачі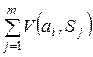
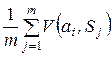
S 1	S 2	S 3	S 4	S 5
a 1 a 2 a 3 a 4 a 5							15,8 15,2 12,4 19,2 16,2	R 1=12,4

¨ Розв’язування.

Принцип Лапласа припускає, що події S ₁, S ₂, S ₃, S ₄, S ₅ рівноймовірні, тобто 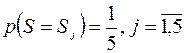. Математичні сподівання витрат при різних альтернативах будуть:

.

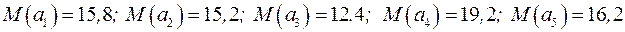Тоді .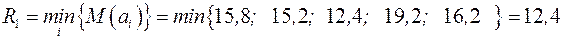

Отже, враховуючи критерій Лапласа, найкращою альтернативою буде альтернатива а ₃. ¨

Дата добавления: 2015-09-02