Використання нерівності Чебишева

Дисперсія неповністю характеризує ступінь ризику, але вона дозволяє в деяких випадках досить чітко визначити граничні шанси менеджера (інвестора, підприємця) при прийнятті економічних рішень. Теоретична основа для цього закладена в нерівності Чебишева: ймовірність того, що випадкова величина відхилиться від свого математичного сподівання за абсолютною величиною більше від додатного числа , не перевищує її дисперсії, поділеної на :

, (11.11)

де R – випадкова величина; m – її математичне сподівання; – дисперсія випадкової величини; – величина відхилення випадкової величини від її математичного сподівання.

Оскільки , то очевидно, що , а отже, .

Розглянемо деяку економічну ситуацію. Нехай інвестиції здійснюються за рахунок кредиту, взятого під відсоток під заставу нерухомості. Знайдемо ймовірність того, що інвестор не зможе повернути борг і позбудеться своєї нерухомості.

Нехай R – випадкова величина ефективності вкладень із математичним сподіванням m і дисперсією V. Тоді ймовірність банкрутства – це ймовірність того, що випадкова величина набуде свого значення, яке відповідає умові:

. (11.12)

В цьому випадку значення ймовірності буде дорівнювати:

. (11.13)

Із проведених алгебраїчних перетворень випливає, що шанс збанкрутувати не перевищує . Тут треба мати на увазі, що раціонально вкладати під кредит можна тільки тоді, коли 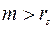, а умова (11.12) виконується лише тоді, коли дисперсія не дуже велика, зокрема .

Для того, щоби при виконанні цих умов, шанс банкрутства був не більше 1 з 9, треба щоби виконувалася нерівність:

. (11.14)

Звідси випливає, щ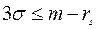о або

. (11.15)

Таким чином, нами отримано правило трьох сигм.

Тут, як один із параметрів ризику, у системі кількісної його оцінки, виступає ймовірність несприятливої події поряд з дисперсією. В зазначеному випадку . Інколи суб’єкта прийняття рішення не задовольняє величина і тоді її встановлюють на рівні 0,001.

Приклад 11.5. Підприємство бере кредит під 20% річних. Експерти оцінюють, що ризик, пов'язаний з коливаннями сподіваного прибутку становить 5%. Оцінити з імовірністю 1/9 рівень сподіваного прибутку, щоб уникнути банкрутства.

♦ Розв’язування.

На підставі отриманої формули (11.15) маємо:

,

тобто рівень сподіваного прибутку повинен бути не меншим за 35%.♦

Розглянемо іншу економічну ситуацію. Нехай кредитор інвестує лише частину свого капіталу, залишаючи іншу частину на заощадження під майже безризиковий відсоток .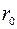

Позначимо:

S – початковий капітал;

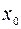– частка, вкладена на заощадження під відсоток .

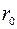Банкрутство можливе, якщо:

.

Звідси,

. (11.16)

У цьому випадку замість , що фігурує в нерівності (11.12), є величина 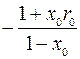. Оцінка за нерівністю Чебишева визначає ризик банкрутства з імовірністю, меншою ніж 1/9 тоді, коли:

,

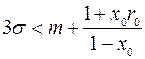
або

. (11.17)

Звідси випливає, що ставка на власний капітал значно безпечніша. Якщо інвестувати весь власний капітал, то достатнім рівнем небанкрутства буде:

. (11.18)

Приклад 11.6.Інвестор,маючи 100 тис грн., вкладає половину капіталу в безризикові цінні папери під відсоткову ставку 35%. Решту грошей він хоче вкласти в папери, які обтяжені ризиком. Ризик цих паперів (середньоквадратичне відхилення) становить 8%.

1. Розрахувати сподівану норму прибутку, обтяженого ризиком цінних паперів, якщо інвестор хоче, щоб шанс банкрутства для нього був меншим за 1/9.

2. Обчислити, яким має бути значення середньоквадратичного відхилення цінних паперів, якщо інвестор вирішив вкласти в них весь капітал. Сподівана (середня) норма прибутку дорівнює 10 %, шанс банкрутства не більший ніж 1/9.

♦ Розв’язування.

1. За умови прикладу , , .

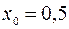Використавши формулу (11.17) одержимо:

–2,11 (–211%).

Тобто сподівана норма доходу цінних паперів, що обтяжені ризиком, має бути не меншою ніж 211%.

2. Відомо, що , . Використавши формулу (11.18), одержимо:

, тобто 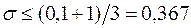або 36,7%.

Отже, ризик має бути не вищим ніж 36,7%. ♦

Дата добавления: 2015-09-02