Оптимізація структури портфеля цінних паперів та оцінка ризику

Методику оптимізації структури портфеля цінних паперів та оцінки ризику представимо з допомогою такого алгоритму. Введемо позначення: i – індекс виду акцій, 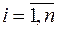, j – індекс ситуації на ринку цінних паперів, 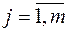; x – ціна придбання акції i -го виду в конкретний період; x_ij – прогнозна ціна акції i -го виду при реалізації j -ої ситуації; P_j – суб’єктивна ймовірність настання j -ої ситуації, 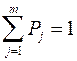; B_j – подія, що означає настання j -ої ситуації на ринку цінних паперів.

Представимо вхідні параметри аналізу структури портфеля цінних паперів у матричній формі (табл. 12.4).

Таблиця12.4

Вхідні параметри аналізу структури портфеля цінних паперів

Вид акцій	Ціна придбання акцій	Прогнозна ціна акцій залежно від ситуації на ринку цінних паперів
В 1	В 2	В	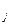Вm
… n	х 10 х 20 … хn 0	х 11 х 21 … хn 1	х 12 х 22 … хn 2	х	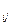х 1 m х 2 m … хnm
Ймовірність ситуації	P 1	P 2	P	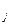Pm

Розглянемо методику можливого визначення сподіваного доходу та ризику кожної акції окремо. Переважно сподіваний дохід за акцією і- го виду обчислюють з допомогою математичного сподівання доходу з окресленого виду акції так:

. (12.15)

Крім того, сподіваний дохід можна визначити з допомогою абсолютного значення (табл. 12.4) або на основі оцінки цього доходу у формі відсотка приросту доходу з кожного виду цінних паперів. Враховуючи введені позначення, формула визначення приросту доходу у відсотковому значенні матиме вигляд:

, (12.16)

де y 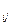– приріст доходу в процентах до ціни акції і -го виду при j -й ситуації на ринку цінних паперів. Сподіваний приріст доходу 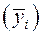в нашому випадку знайдемо за допомогою формули:

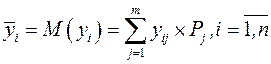. (12.17)

Надалі формулу (12.17) покладено в основу алгоритму відповідних експериментальних розрахунків.

У теорії аналізу структури портфеля цінних паперів під ризиком вкладень розуміють очікуване відхилення прогнозних результатів у вигляді доходів від їх сподіваного значення, тому для оцінки ризику кожної окремої акції або іншого виду цінного паперу можна використовувати дисперсію розподілу її прогнозних доходів. Відомо, що дисперсія дискретної випадкової величини становить математичне сподівання квадрата відхилення випадкової величини і є, в свою чергу, мірою розсіяння значень цієї величини. Для оцінки ризику доцільніше використовувати середнє квадратичне відхилення розподілу доходів за акціями. Його обчислюють як корінь квадратний з дисперсії. Стосовно цінних паперів кожного виду або всього портфеля така оцінка ризику виражає очікуваний інтервал відхилення прогнозного доходу за акцією або за всім портфелем від сподіваного значення доходу за акцією або всього портфеля.

Вибираючи, за інших рівних умов, варіант вкладень з великим середнім квадратичним відхиленням розподілу прогнозних доходів, інвестор сподівається отримати більше, ніж у тому випадку, коли він вибирає варіант з меншим середнім квадратичним відхиленням. Але при цьому інвестор ризикує й отримати менше, ніж у відхиленому варіанті, оскільки згадана величина задає верхню і нижню межі очікуваного інтервалу зміни прогнозних доходів. Отже, для визначення дисперсії прогнозних приростів доходів і їх середніх квадратичних відхилень використаємо формулу:

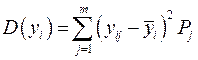, , (12.18)

де D (у_і) – дисперсія, s _і – середнє квадратичне відхилення розподілу приросту прогнозних доходів цінних паперів і -го виду. Надалі під середнім квадратичним s _і будемо розуміти величину ризику.

Отримана пара величин сподіваного приросту доходу та ризику 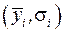може бути використана для кількісного обґрунтування плану вкладень засобів інвестора лише в тому випадку, якщо він хоче придбати тільки один вид акцій або інші цінні папери. При цьому ми маємо на увазі, що будь-який інвестор (ОПР, менеджер), схильний до ризику, завжди вибирає акції з більшим ризиком, а менеджер, несхильний до ризику, – варіант із меншим ризиком.

У випадку, коли між шуканими параметрами мають місце нерівності

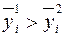і , (12.19)

для прийняття ефективного рішення необхідно використовувати додаткові умови, які адекватно відображали би ставлення менеджера до конкретних варіантів комбінації сподіваного приросту доходу та величини ризику.

З цією метою вводять спеціальну функцію, яка визначена на множині сподіваних приростів доходів і ризиків . Для зазначеної функції властивим є те, що вона зростає до s для менеджерів, схильних до ризику, і спадає до s в протилежному випадку. Крім цього, запропонована функція повинна певним чином відображати систему переваг при дії ОПР. Тобто ОПР, не схильна до ризику, готова прийняти рішення з великим ризиком тільки в тому випадку, якщо їй відповідає велике значення сподіваного приросту доходу, а ОПР, схильна до ризику, може надати перевагу вищому ризику в тому випадку, якщо їй відповідає зниження сподіваного приросту доходу. Згадана функція повинна служити для реального відображення цих переваг ОПР, тобто вона дає їй можливість оцінити перевагу того чи іншого варіанта вкладень у випадку як придбання акцій одного виду, так і сумарної оцінки портфеля цінних паперів.

Проблема аналізу оптимального вибору портфеля цінних паперів становить задачу прийняття рішень в умовах невизначеності, тому для їх розвитку можна використати критерій, який має назву “мінімум середнього ризику”. Зміст його алгоритму полягає у виборі акції виду, для якої математичне сподівання величини ризику матиме мінімальне значення:

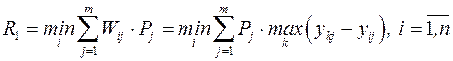. (12.20)

Як бачимо, 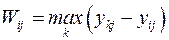є різницею найкращого значення в стовпці j і значення y_ij. За змістом W_ij виражає “співчуття” ОПР через те, що вона не вибрала найкращої дії щодо ситуації B_j.

При аналізі оптимальних фінансових рішень заслуговує певної уваги критерій Ходжеса-Лемана. Для практичного використання цього критерію нам необхідно мати, крім розподілу ймовірностей Р_j відповідних ситуацій, ще і параметр a. Окреслений параметр встановлює баланс між випадками крайнього оптимізму та крайнього песимізму. Значення може визначатися залежно від характеру особи, яка приймає рішення, тобто від того, що їй характерніше, – песимізм чи оптимізм. Вибір оптимальної альтернативи здійснюється відповідно до алгоритму, в основу якого покладено таку закономірність:

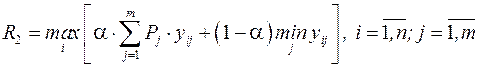. (12.21)

Оцінюючи необхідну початкову інформацію для критерію Ходжеса-Лемана, можна зробити висновок про ступінь його складності. Основним недоліком запропонованого критерію є те, що в його алгоритмі використовується багато суб’єктивних факторів.

У реальних задачах, пов’язаних із формуванням портфеля, виникає потреба в оптимізації його структури та оцінки ризику на випадок, коли він містить принаймні два види цінних паперів. Нехай структура портфеля акцій або інших цінних паперів виражається з допомогою характеристичних показників, що відображають частку вартості акцій зазначеного виду в загальній вартості всього придбаного пакета акцій у період купівлі. Позначимо через 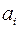– частку акцій і -го виду в загальній вартості портфеля; Q_i – кількість куплених акцій і -го виду, .

Враховуючи вищезгадане та введені позначення, будемо мати:

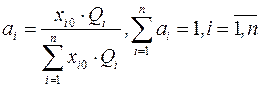. (12.22)

Визначимо прогнозний приріст доходу портфеля акцій у випадку настання j -ої ситуації. Враховуючи формули (12.16) і (12.22), отримаємо:

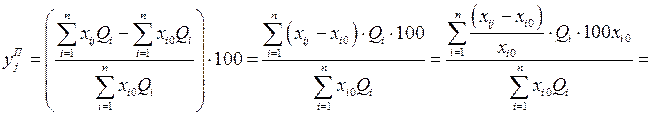
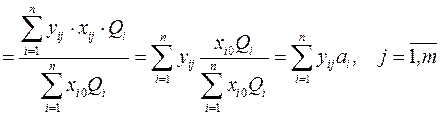. (12.23)

Взявши до уваги структуру портфеля цінних паперів 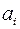(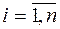), визначимо з допомогою математичного сподівання очікувану величину приросту доходу всього портфеля:

. (12.24)

З формули (12.24) випливає, що сподіваний приріст доходів портфеля цінних паперів є зваженою сумою сподіваних приростів за кожним видом цінних паперів, які входять у його структуру. Ваговими коефіцієнтами виступають значення a_j.

Для оцінки ризику портфеля цінних паперів використаємо середнє квадратичне відхилення розподілу прогнозних приростів доходів портфеля. Отже, ризик портфеля, який містить n видів цінних паперів, оцінюється за формулою

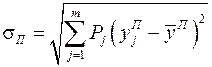, (12.25)

де s _П – ризик портфеля акцій.

Розглянемо випадок, коли n =2, тобто портфель складається з двох видів цінних паперів, і структура його буде характеризуватися числами a ₁і a ₂. Таким чином, ризик портфеля оцінимо за формулою:

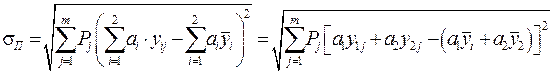. (12.26)

Виконаємо відповідні перетворення для підкореневого виразу, в результаті чого отримаємо:

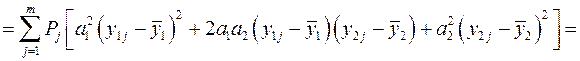(12.27)

.

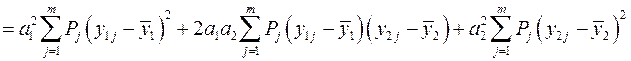Для одержання кінцевого результату введемо величини дисперсії розподілу приростів доходів за акціями першого і другого видів:

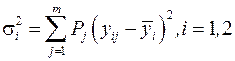, (12.28)

а також коефіцієнт коваріації:

. (12.29)

Як бачимо, коваріація двох випадкових величин становить математичне сподівання добутку відхилення прогнозних приростів доходів за акціями кожного виду від їх сподіваного значення і виражає щільність зв’язку між розподілом приростів доходів за акціями обох видів.

Враховуючи формули (12.27)-(12.29), оцінка ризику портфеля з двох видів цінних паперів матиме вигляд:

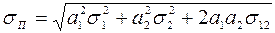. (12.30)

Для аналізу тісноти зв’язку надалі використовуватимемо коефіцієнт кореляції (r_ij), який у нашому випадку буде виражатися з допомогою формули:

, r ₁₂ Î [-1; 1]. (12.31)

З формули (12.31) отримаємо:

. (12.32)

Остаточно одержимо формулу для обчислення ризику портфеля з двох видів акцій:

. (12.33)

Розглянемо кількісний аналіз зв’язку між коефіцієнтом кореляції та приростами доходів. Чим ближче наближається r ₁₂ до +1, тим більша залежність між приростами доходів з обох видів акцій, і навпаки, чим ближче це значення до нуля, тим вона менша. Якщо r ₁₂=0, тоді має місце повна незалежність прогнозних приростів з обох видів акцій. Якщо r ₁₂>0, тоді значення приростів доходів з акцій одночасно або перевищують сподівання значення приростів доходів, або мають значення менше, ніж сподівані прирости доходів з відповідних акцій, тобто є одночасно або порівняно високими, або порівняно низькими. Якщо r ₁₂<0, тоді перевищення значень приросту доходів над сподіваним рівнем з одного виду акцій відповідає зниження приросту доходу нижче від сподіваного рівня для акцій другого виду, і навпаки. Тобто порівняно високим рівням приросту доходу з акцій одного виду відповідають порівняно низькі рівні приросту доходу з акцій другого виду.

Для аналізу ситуації впливу на величини ризику інвестора можливого перерозподілу або диверсифікації його засобів між різними ризикованими сценаріями (проектами) з гарантованими приростами доходів надалі будемо використовувати формулу (12.33).

Припустимо, що інвестор має два ризикованих сценарії можливих вкладень. Перший полягає у придбанні акцій двох видів, а другий, крім цього, передбачає вклад грошей у банк під фіксований процент річних. Для спрощення приймемо 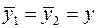і . Отже, в окресленому випадку при купівлі інвестором акцій тільки одного виду сподіваний рівень доходу дорівнюватиме y, а ризик – s. Проаналізуємо другий випадок, коли портфель цінних паперів інвестора складається з акцій двох видів і вкладень у банк. Позначимо через 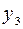– банківський річний процент, 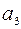– частку коштів вкладених у банк.

Отже, сподіваний приріст доходу портфеля цінних паперів буде рівний:

. (12.34)

Аналіз (12.36) показує, що збільшення або зменшення сподіваного приросту доходу у цьому випадку залежить від співвідношення процентів як банківського, так і сподіваного приросту доходу з акцій. Тобто, якщо , тоді сподіваний приріст доходу портфеля більший, ніж у першому випадку. Якщо 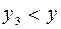, тоді вкладати капітал у банк не вигідно.

Використавши формулу (12.33) і врахувавши, що , знайдемо величину оцінки ризику сформованого портфеля цінних паперів

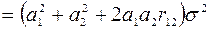. (12.35)

Аналіз показує, що зниження ризику портфеля порівняно з ризиком вкладень тільки в один вид акцій буде лише за умови, коли , тобто повинно мати місце:

. (12.36)

Враховуючи, що 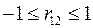, отримаємо:

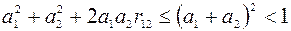, якщ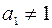о або 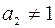. (12.37)

Звідси, нерівність (12.36) виконується для будь-яких допустимих структур портфеля, крім тих, коли інвестор купує тільки один вид акцій (а ₁=1, а ₂=0 або а ₁=0, а ₂=1). Отже, якщо портфель містить акції обох видів у будь-якому співвідношенні, то ризик портфеля буде меншим, ніж ризик кожного цінного паперу зокрема. У випадку вкладення інвестором капіталу в банк (а ₃=1–(а ₁+ а ₂)>0) вираз (а ₁+ а ₂) зменшиться, і це приводить до зниження ризику портфеля порівняно з ризиком акцій одного виду.

Перейдемо до розгляду конкретної фінансової ситуації, яка полягає у формуванні оптимального портфеля цінних паперів з такими вхідними даними:

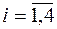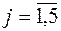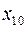, , =2,5 грн., =3,0 грн., 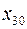=4,0 грн.,

=6,0 грн.; Р ₁=0,1, Р ₂=0,2, Р ₃=0,25, Р ₄=0,2, Р ₅=0,25;

.

Взявши в основу обчислень формулу (12.18), отримаємо розподіл прогнозних приростів доходів у процентному виразі (табл. 12.5). Далі, користуючись формулами (12.19) і (12.20), отримаємо значення сподіваного приросту та величини ризику з кожного виду акцій (табл. 12.5).

Таблиця12.5

Аналіз розподілу приростів доходу акцій i їх характеристики

Акції

Приріст доходу акцій залежно від ситуації,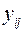

Сподіваний приріст доходу,

Ризик

В 1

В 2

В 3

В 4

В 5

sі

8,0 6,67 25,0 15,0

4,0 26,67 5,0 11,67

8,0 3,33 2,5 8,33

16,0 16,67 12,5 3,33

12,0 13,33 17,5 5,0

9,8 13,5 11,0 7,83

4,09 8,19 7,47 3,77

Ймовірність ситуації

Р1=0,1

Р2=0,2

Р3=0,25

Р4=0,2

Р5=0,25

Розглянемо аналіз шести можливих варіантів структури портфеля цінних паперів, включаючи в кожний два види акцій: портфель-1 містить акції першого та другого виду; портфель-2 – першого та третього; портфель-3 – першого і четвертого, портфель-4 – другого та третього, портфель-5 – другого і четвертого, портфель-6 – третього та четвертого. В основу алгоритму покладено формули (12.24) і (12.30), при цьому будемо дискретно змінювати структуру портфеля щодо коефіцієнтів а_і (і =1, 2, 3,4) з кроком 0,1. Отримані числові результати подамо у вигляді табл. 12.6.

Аналіз даних табл. 12.6 показує, що при зміні сподіваного приросту доходу ризик портфеля, залежно від його структури, може зростати або спадати.

Таблиця 12.6

Аналіз приросту доходів i ризику портфелів цінних паперів

Портфель-1	Портфель-2	Портфель-3
Структура	Сподіваний приріст доходу	Ризик	Структура	Сподіваний приріст доходу	Ризик	Структура	Сподіваний приріст доходу	Ризик
Акція 1	Акція 2	Акція 1	Акція 2	Акція 1	Акція 2
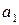
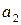
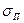
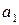
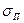
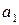
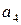
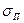
0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1	0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9	9,8 10,17 10,54 10,91 11,28 11,65 12,02 12,39 12,76 13,13 13,50	4,094 3,638 3,408 3,449 3,752 4,263 4,916 5,663 6,471 7,320 8,197	0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1	0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9	9,8 9,92 10,04 10,16 10,28 10,40 10,52 10,64 10,76 10,88 11,00	4,094 4,074 4,165 4,358 4,642 5,001 5,420 5,886 6,389 6,920 7,475	0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1	0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9	9,8 9,6 9,41 9,21 9,01 8,82 8,62 8,42 8,23 8,03 7,83	4.094 3,37 2,665 1,997 1,42 1,091 1,227 1,721 2,359 3,051 3,768
Портфель-4	Портфель-5	Портфель-6
Структура	Сподіваний приріст доходу	Ризик	Структура	Сподіваний приріст доходу	Ризик	Структура	Сподіваний приріст доходу	Ризик
Акція 1	Акція 2	Акція 1	Акція 2	Акція 1	Акція 2
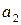
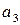
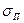
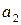
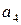
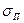
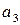
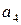
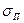
0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1	0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9	13,5 13,25 13,0 12,75 12,5 12,25 12,0 11,75 11,5 11,25 11,0	8,197 7,378 6,652 6,055 5,626 5,406 5,421 5,668 6,121 6,736 7,475	0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1	0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9	13,5 12,93 12,37 11,8 11,23 10,67 10,1 9,53 8,97 8,4 7,83	8,197 7,401 6,63 5,891 5,199 4,577 4,054 3,675 3,487 3,52 3,768	0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1	0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9	11,0 10,68 10,37 10,05 9,73 9,42 9,1 8,78 8,47 8,15 7,83	7,475 6,717 5,985 5,291 4,65 4,09 3,646 3,365 3,289 3.431 3,768

Припустимо, що інвестор хоче мати структуру портфеля з мінімальним ризиком. Наприклад, візьмемо другий портфель, який містить акції першого та третього видів.

Отже, у нашому випадку (12.32) матиме вигляд:

. (12.38)

Поклавши у формулу (12.32) а ₃=1– а ₁, отримаємо залежність ризику портфеля від однієї змінної а ₁:

Для знаходження екстремуму окресленої функції знайдемо часткову похідну і прирівняємо до нуля. Одержимо:

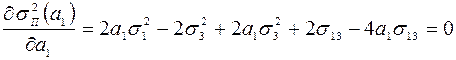
або . (12.39)

Звідси, .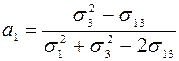

Така структура портфеля дає можливість отримати оптимальний сподіваний приріст доходу (12.24) за мінімального ризику (12.38).

Проведені розрахунки дають змогу сформувати шість портфелів цінних паперів. Отримані результати подаємо у таблиці 12.7.

Таблиця12.7

Аналіз оптимальної структури портфеля цінних паперів з мінімальним ризиком

Портфель	Структура портфеля акцій	Сподіваний приріст доходу	Мінімальний ризик
1. 1-2 2. 1-3 3. 1-4 4. 2-3 5. 2-4 6. 3-4	а 1=0,765 а 1=0,932 а 1=0,478 а 2=0,456 а 2=0,165 а 3=0,215	а 2=0,235 а 3=0,068 а 4=0,522 а 3=0,544 а 4=0,835 а 4=0,785	10,6695 9,8816 8,7732 12,140 8,7681 8,5139	3,3903 4,0686 1,0773 5,3831 3,4725 3,2860

Аналіз таблиці показує, що з шести сформованих портфелів оптимальним з точки зору мінімального ризику є третій портфель. Припустимо, що інвестор асигнує на придбання акцій 17500 грн. і планує мати третій портфель. Тоді він повинен купити на 8365 грн. (0,478´17500=8365) акцій першого виду та на 9135 грн. (0,544´17500=9135) акцій четвертого виду. Враховуючи початкову вартість акцій, інвесторові необхідно придбати 3346 акцій першого емітента та 1522 – акцій четвертого емітента.

Наведена методика у доступній формі допомагає зрозуміти основні результати інвестиційних процесів у теорії вибору структури портфеля цінних паперів. Інвестор завжди може отримати вигідну структуру портфеля, яка забезпечить йому мінімальний ризик.

Питання для самоконтролю

1. Що складає основу логічної структури теорії прийняття рішень?

2. Опишіть основні елементи, що характеризують управлінське рішення.

3. Що спільного і яка відмінність у прийнятті рішень в умовах ризику та невизначеності?

4. Які критерії покладені в основу прийняття рішень в умовах ризику?

5. Опишіть алгоритм прийняття рішень в умовах ризику за допомогою критерію “сподіване значення”.

6. У чому відмінність критеріїв “сподіване значення” та “сподіване значення - дисперсія”?

7. Чи дає можливість отримати оптимальне рішення при використанні критерію “граничний рівень”?

8. У чому полягає компроміс при прийнятті рішень з допомогою критерію “граничний рівень”?

9. Опишіть виробничу ситуацію, пов’язану з використанням експериментальних даних при прийнятті рішень в умовах ризику.

10. Запишіть для загального випадку формулу повної ймовірності та формулу Байєса.

11. Опишіть алгоритм методу «дерева цілей».

12. Побудуйте логічну схему процедури прийняття рішень у вигляді “дерева цілей”.

13. Запишіть формулу Байєса для загального випадку. Який її прикладний зміст?

14. Опишіть алгоритм оптимізації структури портфеля цінних паперів з урахуванням ризиків.

15. Запишіть формулу оцінки ризику портфеля цінних паперів.

16. Як виглядає формула оцінки ризику портфеля цінних паперів, коли є дві акції?

Дата добавления: 2015-09-02