Основные соотношения двойственности

I. Если решение исходной задачи на максимум существует, то решение двойственной задачи на минимум точно ему равно:

Р_max= С_min

Теневые цены для двойственной задачи - это оптимальное решение x_j для прямой ЛП-задачи.

II. Для оптимальных планов исходной и двойственной задач:
1. Если

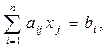
т.е. i-й ресурс использован полностью при производстве про­дукции по оптимальному плану, то его теневая цена больше нуля

y_i > 0.

2. Если же

т.е. i-й ресурс не полностью используется при производстве продукции по оптимальному плану, то его теневая цена равна 0:

y_j = 0.

3. Если x_j>0,

т.е. если j-й продукт вошел в оптимальный план, то в соответ­ствующем ограничении двойственной задачи реализуется знак равенства, т.е. выручка от продажи ресурсов, идущих на про­изводство единицы этого продукта, равна прибыли от его про­изводства:

4. Если же x_j =0,

т.е. если j-й продукт не входит в оптимальный план, то в соот­ветствующем ограничении двойственной задачи реализуется знак "больше", т.е. выручка от продажи ресурсов, идущих на производство единицы этого продукта, больше прибыли от его производства:

III. Теневые цены y_jпоказывают, на сколько увеличится значение Р_max, если запасы ресурса увеличить на единицу:

Заключение

Максимум или минимум целевой функции достигается в одной из угловых точек области допустимых планов. Эта точка является пересечением границ тех ресурсов, которые при оптимальном плане рас­ходуются полностью.

Существует определенный интервал устойчивости, в котором из­менение целевых коэффициентов не приводит к изменению оптималь­ного решения. При выходе за пределы интервала устойчивости опти­мальное решение может измениться очень сильно.

Теневая цена ресурса показывает, на сколько изменится прибыль от производства при изменении данного ресурса на единицу. Она ха­рактеризует субъективную ценность ресурса с точки зрения произво­дителя и не имеет ничего общего с рыночной ценой ресурса. В част­ности, если ресурс имеется в избытке (не используется полностью в оптимальном плане), его теневая цена равна нулю.

Если правая часть ограничения имеет другой смысл, нежели запас ресурса, ее теневая цена может быть даже отрицательна (увеличение правой части ограничения может приводить к снижению прибыли).

Так же как и в случае целевых коэффициентов, существует некото­рый интервал устойчивости, в котором изменение величины ресурса (или изменение правых частей ограничений) не приводит к изменению теневых цен. В этом интервале изменения ресурсов изменение прибыли (или целевой функции) может быть рассчитано по формуле

где ΔР - изменение прибыли, у_i - теневая цена, а Δb_i - изменение i-го ресурса.

За пределами интервала устойчивости теневая цена изменится скачком и применение указанной формулы для оценки прибыли будет невозможным.

Отчет об устойчивости MS-Excel состоит из двух частей (двух таб­лиц).

В первой таблице ("Изменяемые ячейки") представлены интерва­лы устойчивости для целевых коэффициентов и нормированные сто­имости (reduced costs). Если некоторый продукт в задаче об оптималь­ном плане производства не входит в оптимальный план, то его норми­рованная стоимость меньше нуля, а ее величина показывает, на сколько нужно увеличить норму прибыли этого продукта, чтобы он вошел в оп­тимальный план.

Во второй таблице представлена информация о теневых ценах и интервалах устойчивости этих цен при изменении запасов ресурсов.

Для ЛП-задач характерна высокая чувствительность решения к малым изменениям параметров. Малые изменения параметров приводят к огромным изменениям в наборе оптимальных переменных ре­шения. При этом значения целевой функции, отвечающие этим раз­личным оптимальным решениям, различаются очень незначительно. Это означает, что для ЛП-моделей, существует, как правило, множествo альтернативных, близких к оптимальному решений.

Наличие альтернативных решений позволяет менеджеру выбрать такoe, которое в большей степени отвечает тем или иным неформализуемым требованиям и условиям, всегда присутствующим в практике принятия решений.

Дата добавления: 2015-08-21